题目内容
12.在等腰三角形ABC中,AB=AC,一腰上的中线BD将三角形的周长分成12和6两部分,求这个等腰三角形的腰长及底边长.分析 因为两个数据具体是哪一部分的不明确,所以分12是腰长加腰长的一半和6是腰长加腰长的一半两种情况讨论求解.
解答 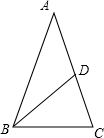 解:如图,
解:如图,
根据题意,
(1)若12是腰长加腰长的一半,
则腰长为:12×$\frac{2}{3}$=8,
底边长为:6-8×$\frac{1}{2}$=2,
此时三角形的三边长为8、8、2,
能组成三角形;
(2)若6是腰长加腰长的一半,
则腰长为:6×$\frac{2}{3}$=4,
底边长为:12-$\frac{1}{2}$×4=10,
此时,三角形的三边长为4、4、10不能组成三角形.
故该等腰三角形的腰长和底边长分别为8,2.
点评 本题考查了等腰三角形的性质;解题中应用了等腰三角形腰长相等的性质和分类讨论的思想,要注意根据三角形的三边关系判定是否能够组成三角形.

练习册系列答案
相关题目
3.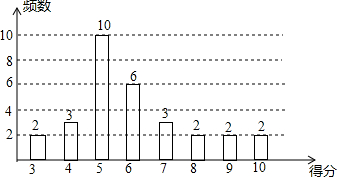 为了普及环保知识,增强环保意识,某中学随机抽取了30名学生参加环保知识测试,得分(10分制)如图所示,假设得分值的中位数为m,众数为n,平均数为$\overline x$,则( )
为了普及环保知识,增强环保意识,某中学随机抽取了30名学生参加环保知识测试,得分(10分制)如图所示,假设得分值的中位数为m,众数为n,平均数为$\overline x$,则( )
 为了普及环保知识,增强环保意识,某中学随机抽取了30名学生参加环保知识测试,得分(10分制)如图所示,假设得分值的中位数为m,众数为n,平均数为$\overline x$,则( )
为了普及环保知识,增强环保意识,某中学随机抽取了30名学生参加环保知识测试,得分(10分制)如图所示,假设得分值的中位数为m,众数为n,平均数为$\overline x$,则( )| A. | m=n=$\overline x$ | B. | m=n<$\overline x$ | C. | m<n<$\overline x$ | D. | n<m<$\overline x$ |
4.下列角度中不是多边形内角和的只有( )
| A. | 540° | B. | 720° | C. | 960° | D. | 1080° |
1.若0<α<30°,则sinα,cosα,tanα的大小关系是( )
| A. | sinα<cosα<tanα | B. | sinα<tanα<cosα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
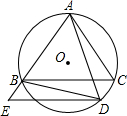 ⊙O是△ABC的外接圆,且AB=AC,点D在$\widehat{AB}$上运动(不与B,C点重合),过点D作DE∥BC,与AB的延长线交于点E,连接AD、BD.
⊙O是△ABC的外接圆,且AB=AC,点D在$\widehat{AB}$上运动(不与B,C点重合),过点D作DE∥BC,与AB的延长线交于点E,连接AD、BD.