题目内容
9．
如图，△ACB中，∠C=90°，BD平分∠ABC交AC于点D，若AB=12，CD=6，则S△ABD为36．
分析 过点D作DE⊥AB于点E，根据角的平分线上的点到角的两边的距离相等，得DE=DC=4，再根据三角形的面积计算公式得出△ABD的面积．
解答 
解：如图，过点D作DE⊥AB于点E，
∵BD平分∠ABC，
又∵DE⊥AB，DC⊥BC，
∴DE=DC=4，
∴△ABD的面积=$\frac{1}{2}$•AB•DE=$\frac{1}{2}$×12×6=36．
故答案为：36．
点评 本题主要考查了角平分线的性质与三角形的面积计算公式．作出辅助线是正确解答本题的关键．
练习册系列答案
相关题目
20．下列各式可以写成完全平方式的多项式有（ ）
| A． | x2+xy+y2 | B． | x2-xy+$\frac{1}{4}{y}^{2}$ | C． | x2+2xy+4y2 | D． | $\frac{1}{4}{x}^{4}-x+1$ |
17．
如图，A，B两地被池塘隔开，小明通过下列方法测出了A，B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A，B间的距离，有关他这次探究活动的描述错误的是（ ）
如图，A，B两地被池塘隔开，小明通过下列方法测出了A，B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A，B间的距离，有关他这次探究活动的描述错误的是（ ）| A． | MN∥AB | |
| B． | AB=24m | |
| C． | △CMN∽△CAB | |
| D． | △CMN与四边形ABMN的面积之比为1：2 |
如图，∠A=70°，O是AB上一点，直线OD与AB所夹的∠BOD=78°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转8°．
1．
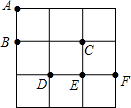如图，在3×3的方格中，点A、B、C、D、E、F都是格点，从A、D、E、F四点中任意取一点，以所取点及B、C为顶点画三角形，所画三角形是直角三角形的概率是（ ）
如图，在3×3的方格中，点A、B、C、D、E、F都是格点，从A、D、E、F四点中任意取一点，以所取点及B、C为顶点画三角形，所画三角形是直角三角形的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{2}{3}$ |
如图，AD=$\frac{1}{2}$DB，E是BC的中点，BE=$\frac{1}{4}$AC=4cm，