题目内容
 如图,△ABC中,∠ACB=90°,AC=BC,点F在BA的延长线上,以AF为边作正方形ADEF,连接EB,点M为EB的中点,连接DM并延长交AB于N,连接CM.
如图,△ABC中,∠ACB=90°,AC=BC,点F在BA的延长线上,以AF为边作正方形ADEF,连接EB,点M为EB的中点,连接DM并延长交AB于N,连接CM.(1)若BN=2,AC=3
| 2 |
(2)求证:CM=
| 1 |
| 2 |
考点:全等三角形的判定与性质,勾股定理,等腰直角三角形,正方形的性质
专题:计算题
分析:(1)由M为EB的中点,得到EM=BM,根据ED与AB平行,得到两对内错角相等,利用AAS得到三角形DEM与三角形MNB全等,利用全等三角形对应边相等得到DE=BN,再由正方形ADEF,得到EF=AF=BN=2,根据三角形ABC为等腰直角三角形,由AC求出AB的长,再由FA+AB求出FB的长,在直角三角形BEF中,利用勾股定理即可求出BE的长;
(2)连接CD,CN,根据NB=AD,BC=AC,且夹角都为45°,利用SAS得到三角形ACD与三角形BCN全等,利用全等三角形对应边相等得到CD=CN,对应角相等得到∠ACD=∠BCN,利用等式的性质得到∠DCN为直角,即三角形DCN为等腰直角三角形,根据M为DN的中点,利用直角三角形斜边上的中线等于斜边的一半即可得证.
(2)连接CD,CN,根据NB=AD,BC=AC,且夹角都为45°,利用SAS得到三角形ACD与三角形BCN全等,利用全等三角形对应边相等得到CD=CN,对应角相等得到∠ACD=∠BCN,利用等式的性质得到∠DCN为直角,即三角形DCN为等腰直角三角形,根据M为DN的中点,利用直角三角形斜边上的中线等于斜边的一半即可得证.
解答: (1)解:∵M为EB的中点,
(1)解:∵M为EB的中点,
∴EM=BM,
∵四边形ADEF为正方形,
∴ED∥BN,AD=AF=EF=ED,
∴∠DEM=∠NBM,∠EDM=∠BNM,
在△DEM和△NBM中,
,
∴△DEM≌△NBM(AAS),
∴DM=NM,ED=BN=2,
∵△ABC为等腰直角三角形,AC=3
,
∴AB=
AC=6,
在Rt△EFB中,EF=2,FB=FA+AB=2+6=8,
根据勾股定理得:BE=
=2
;
(2)证明:连接CD,CN,
∵△ABC为等腰直角三角形,且∠DAB=90°,
∴∠DAC=∠NBC=45°,
在△ADC和△BNC中,
,
∴△ADC≌△BNC(SAS),
∴∠ACD=∠BCN,
∵∠ACN+∠BCN=90°,
∴∠ACN+∠ACD=90°,即∠DCN=90°,
∵M为DN的中点,即CM为斜边DN上的中线,
∴CM=
DN.
 (1)解:∵M为EB的中点,
(1)解:∵M为EB的中点,∴EM=BM,
∵四边形ADEF为正方形,
∴ED∥BN,AD=AF=EF=ED,
∴∠DEM=∠NBM,∠EDM=∠BNM,
在△DEM和△NBM中,
|
∴△DEM≌△NBM(AAS),
∴DM=NM,ED=BN=2,
∵△ABC为等腰直角三角形,AC=3
| 2 |
∴AB=
| 2 |
在Rt△EFB中,EF=2,FB=FA+AB=2+6=8,
根据勾股定理得:BE=
| EF2+FB2 |
| 17 |
(2)证明:连接CD,CN,
∵△ABC为等腰直角三角形,且∠DAB=90°,
∴∠DAC=∠NBC=45°,
在△ADC和△BNC中,
|
∴△ADC≌△BNC(SAS),
∴∠ACD=∠BCN,
∵∠ACN+∠BCN=90°,
∴∠ACN+∠ACD=90°,即∠DCN=90°,
∵M为DN的中点,即CM为斜边DN上的中线,
∴CM=
| 1 |
| 2 |
点评:此题考查了全等三角形的判定与性质,正方形的性质,等腰直角三角形的性质,以及直角三角形斜边上的中线性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,半圆的直径AB=10,弦CD∥AB,且∠CAD=30°,则图中阴影部分的面积为
如图,半圆的直径AB=10,弦CD∥AB,且∠CAD=30°,则图中阴影部分的面积为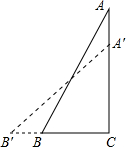 在一堂数学课上,李老师对课本上的一道习题进行了改编,改编后的习题为:一架梯子AB斜靠在竖直的墙AC上,这时B到墙角C距离为1米,如果梯子的顶端沿墙下滑0.2米,此时点B将向外移动0.4米,(参考数据:
在一堂数学课上,李老师对课本上的一道习题进行了改编,改编后的习题为:一架梯子AB斜靠在竖直的墙AC上,这时B到墙角C距离为1米,如果梯子的顶端沿墙下滑0.2米,此时点B将向外移动0.4米,(参考数据: 某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导教师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频率分布直方图,根据图中提供的信息回答下列问题:
某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导教师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频率分布直方图,根据图中提供的信息回答下列问题: 如图,在矩形ABCD中,AB=3,E为AD中点,AC与BE相交于点P,点B坐标为(2,2),反比例函数y=
如图,在矩形ABCD中,AB=3,E为AD中点,AC与BE相交于点P,点B坐标为(2,2),反比例函数y=