题目内容
如图，半圆的直径AB=10，弦CD∥AB，且∠CAD=30°，则图中阴影部分的面积为考点：扇形面积的计算
专题：
分析：连接OC，OD，判断出阴影部分的面积=扇形OCD的面积，根据扇形的面积公式即可求解．
解答：
解：连接OC，OD，
∵∠CAD=30°，
∴∠COD=60°，
∵AB∥CD，
∴△ACD的面积=△COD的面积，
∴阴影部分的面积=弓形CD的面积+△COD的面积=扇形OCD的面积=
=
．
故答案为：
．
解：连接OC，OD，∵∠CAD=30°，
∴∠COD=60°，
∵AB∥CD，
∴△ACD的面积=△COD的面积，
∴阴影部分的面积=弓形CD的面积+△COD的面积=扇形OCD的面积=
| 60π×52 |
| 360 |
| 25π |
| 6 |
故答案为：
| 25π |
| 6 |
点评：本题主要考查了扇形的面积公式，正确理解阴影部分的面积=扇形COD的面积是解题的关键．
练习册系列答案
相关题目
若函数y1=x-1和函数y2=
的图象相交于点M（m，1），N（n，-2），若y1＞y2，则x的取值范围是（ ）
| 2 |
| x |
| A、x＜-1或0＜x＜2 |
| B、x＜-1或x＞2 |
| C、-1＜x＜0或0＜x＜2 |
| D、-1＜x＜0或x＞2 |
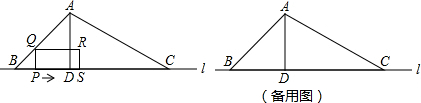
如图，△ABC中，∠ACB=90°，AC=BC，点F在BA的延长线上，以AF为边作正方形ADEF，连接EB，点M为EB的中点，连接DM并延长交AB于N，连接CM．