题目内容
19．
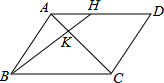如图，H为平行四边形ABCD中AD边上一点，且AH=$\frac{1}{2}$DH，AC和BH交于点K，则AK：KC等于（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 2：3 |
分析 根据“AH=$\frac{1}{2}$DH”求出AH：AD即AE：BC的值是1：3，再根据相似三角形对应边成比例求出AK：KC的值．
解答 解：∵AH=$\frac{1}{2}$DH，
∴$\frac{AH}{AD}=\frac{1}{3}$，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴△AHK∽△CBK，
∴$\frac{AK}{KC}$=$\frac{1}{3}$，
故选B．
点评 本题考查了相似三角形的判定和性质，平行四边形的性质，比例式的变形是解题的关键．
练习册系列答案
相关题目
如图，抛物线y=kx2-2kx-3k（k＞0）与x轴交于A、B两点，与y轴交于C点．
14．下列几种说法中，正确的是（ ）
| A． | 最小的自然数是1 | |
| B． | 在一个数前面加上“-”号所得的数是负数 | |
| C． | 任意有理数a的倒数是$\frac{1}{a}$ | |
| D． | 任意有理数a的相反数是-a |
11．已知某三角形一边长是方程x2-6x+5=0的一个根，另两边的长为2和4，则该三角形的周长为（ ）
| A． | 11 | B． | 7 | C． | 7或11 | D． | 以上都不对 |
8．
如图，在△ABC中，∠B+∠C=110°，AD平分∠BAC，交BC于D，DE∥AB，则∠ADE的度数为（ ）
如图，在△ABC中，∠B+∠C=110°，AD平分∠BAC，交BC于D，DE∥AB，则∠ADE的度数为（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 45° |