已知某三角形一边长是方程x2-6x+5=0的一个根.另两边的长为2和4.则该三角形的周长为( )A．11B．7C．7或11D．以上都不对题目和参考答案——青夏教育精英家教网—

题目内容

11．已知某三角形一边长是方程x²-6x+5=0的一个根，另两边的长为2和4，则该三角形的周长为（　　）

A．

B．

C．

7或11

D．

以上都不对

分析首先利用因式分解法求出方程的根，再根据三角形三边关系定理，确定第三边的长，进而求其周长．

解答解：解方程x²-6x+5=0得：x₁=1，x₂=5，
∵另两边的长为2和4，
∴2＜第三边的边长＜6，
∴第三边的边长为5．
∴这个三角形的周长是2+4+5=11．
故选A．

点评此题考查了因式分解法解一元二次方程和三角形的三边关系，要注意已知三角形的两边，则第三边的范围是：大于已知的两边的差，而小于两边的和．

练习册系列答案

创新考王完全试卷系列答案

期末复习检测系列答案

超能学典单元期中期末专题冲刺100分系列答案

相关题目

1．

一个几何体由大小相同小立方块搭成，从上面看到几何体形状如图所示，其中小正方体中数字表示该位置上小立方块个数，请画出从正面看、从左面看这个几何体的形状图．

2．

如图，已知一次函数y₁=（m-1）x+2与正比例函数y₂=2x图象相交于点A（2，n），y₁=（m-1）x+2与x轴交于点B．
（1）求出m、n的值；
（2）求出△ABO的面积．

19．

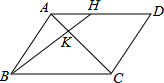如图，H为平行四边形ABCD中AD边上一点，且AH=$\frac{1}{2}$DH，AC和BH交于点K，则AK：KC等于（　　）

6．计算：
（1）计算：17-8÷（-2）²+4×（-3）
（2）先化简，再求值：-（x²-1）-2（x²-2x-$\frac{1}{2}$），其中x=-2．

16．计算下列各题
（1）$\root{3}{125}$-$\sqrt{64}$÷|-$\frac{1}{2}$|
（2）-2⁴+（1-$\frac{1}{3}$+$\frac{1}{12}$）×（-6）²．

3．“a，b是实数，|a|+$\sqrt{{b}^{2}}$≥0“这一事件是（　　）

20．

如图，△ABC中，∠C=90°，AD是角的平分线，CD=3，BD=4，AD=7，点P是AB上一动点从A向B运动，则DP的取值范围是3≤DP≤7．

1．已知AB是⊙O的直径，点C在⊙O上，∠CBA=30°，则∠CAB的度数是（　　）

试题分类