题目内容
7. 如图,抛物线y=kx2-2kx-3k(k>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=kx2-2kx-3k(k>0)与x轴交于A、B两点,与y轴交于C点.(1)请求出抛物线顶点M的坐标(用含k的代数式表示),A、B两点的坐标;
(2)试探究,△BCM与△ABC的面积比值是否不变?若不变,试求出这个比值;若会变,请说明理由.
分析 (1)运用配方法把二次函数一般式化为顶点式,求出顶点坐标,解方程求出A、B两点的坐标;
(2)过M作MD⊥x轴于点D,根据三角形的面积公式计算即可.
解答 解:(1)∵y=kx2-2kx-3k=k(x-1)2-4k,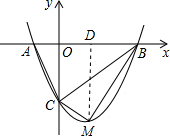
∴抛物线顶点M坐标为(1,-4k),
∵抛物线y=kx2-2kx-3k(k>0)与x轴交于A、B两点,
∴当y=0时,kx2-2kx-3k=0,
∵k>0,∴x2-2x-3=0,
解得:x1=-1,x2=3,
则A、B两点的坐标为(-1,0),(3,0);
(2)不变,
当x=0时,y=-3k,即C(0,-3k),
∴S△ABC=$\frac{1}{2}$×|3-(-1)|×|-3k|=6|k|=6k,
过M作MD⊥x轴于点D,
则有OD=1,BD=OB-OD=2,MD=|-4k|=4k,
∴S△BCM=S△BDM+S梯形OCMD-S△BOC=$\frac{1}{2}$BD•DM+$\frac{1}{2}$(OC+DM)•OD-$\frac{1}{2}$OB•OC
=$\frac{1}{2}$×2×4k+$\frac{1}{2}$×(3k+4k)×1-$\frac{1}{2}$×3×3k=3k,
∴S△BCM:S△ABC=3k:6k=1:2.
∴△BCM与△ABC的面积比不变,为1:2.
点评 本题考查的是二次函数的性质、抛物线与x轴的交点的求法,正确运用配方法把二次函数一般式化为顶点式是解题的关键,注意方程思想的应用.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了52个谷穗作为样本,量得它们的长度(单位:cm).对样本数据适当分组后,列出了如下频数分布表:
(1)请你在图1,图2中分别绘出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;
(3)求这块试验田里穗长在5.5≤x<7范围内的谷穗的概率.
| 穗长 | 4.5≤x<5 | 5≤x<5.5 | 5.5≤x<6 | 6≤x<6.5 | 6.5≤x<7 | 7≤x<7.5 |
| 频数 | 4 | 8 | 12 | 13 | 10 | 5 |
(2)请你对这块试验田里的水稻穗长进行分析;
(3)求这块试验田里穗长在5.5≤x<7范围内的谷穗的概率.

19.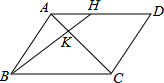 如图,H为平行四边形ABCD中AD边上一点,且AH=$\frac{1}{2}$DH,AC和BH交于点K,则AK:KC等于( )
如图,H为平行四边形ABCD中AD边上一点,且AH=$\frac{1}{2}$DH,AC和BH交于点K,则AK:KC等于( )
 如图,H为平行四边形ABCD中AD边上一点,且AH=$\frac{1}{2}$DH,AC和BH交于点K,则AK:KC等于( )
如图,H为平行四边形ABCD中AD边上一点,且AH=$\frac{1}{2}$DH,AC和BH交于点K,则AK:KC等于( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
17.若关于x的不等式组$\left\{\begin{array}{l}{2x≥3}\\{x+a≤2}\end{array}\right.$有解,则实数a的取值范围为( )
| A. | a≤$\frac{1}{2}$ | B. | a<$\frac{1}{2}$ | C. | a≥$\frac{1}{2}$ | D. | a>$\frac{1}{2}$ |
 如图,已知一次函数y1=(m-1)x+2与正比例函数y2=2x图象相交于点A(2,n),y1=(m-1)x+2与x轴交于点B.
如图,已知一次函数y1=(m-1)x+2与正比例函数y2=2x图象相交于点A(2,n),y1=(m-1)x+2与x轴交于点B. 如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D.
如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D.