题目内容
8．
如图，在△ABC中，∠B+∠C=110°，AD平分∠BAC，交BC于D，DE∥AB，则∠ADE的度数为（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 45° |
分析 由∠B+∠C=110°，根据三角形内角和求得∠BAC=70°，由AD平分∠BAC，可得∠BAD=35°，由DE∥AB，根据平行线的性质及可求得结论．
解答 解：∵∠B+∠C=110°，
∴∠BAC=180°-（∠B+∠C）=70°，
∵AD平分∠BAC，
∴∠BAD=$\frac{1}{2}$∠BAC=35°，
∵DE∥AB，
∴∠ADE=∠BAD=35°，
故选B．
点评 本题主要考查了三角形内角和定理，角平分线的性质，平行线的性质，熟练掌握平行线的性质是解决问题的关键．
练习册系列答案
相关题目
19．
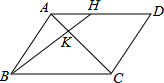如图，H为平行四边形ABCD中AD边上一点，且AH=$\frac{1}{2}$DH，AC和BH交于点K，则AK：KC等于（ ）
如图，H为平行四边形ABCD中AD边上一点，且AH=$\frac{1}{2}$DH，AC和BH交于点K，则AK：KC等于（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 2：3 |
3．“a，b是实数，|a|+$\sqrt{{b}^{2}}$≥0“这一事件是（ ）
| A． | 必然事件 | B． | 不确定事件 | C． | 不可能事件 | D． | 随机事件 |
如图，△ABC中，∠C=90°，AD是角的平分线，CD=3，BD=4，AD=7，点P是AB上一动点从A向B运动，则DP的取值范围是3≤DP≤7．
17．若关于x的不等式组$\left\{\begin{array}{l}{2x≥3}\\{x+a≤2}\end{array}\right.$有解，则实数a的取值范围为（ ）
| A． | a≤$\frac{1}{2}$ | B． | a＜$\frac{1}{2}$ | C． | a≥$\frac{1}{2}$ | D． | a＞$\frac{1}{2}$ |
已知：如图所示，O为数轴的原点，A，B分别为数轴上的两点，A点对应的数为-30，B点对应的数为100．