题目内容
13.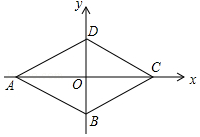 如图,已知菱形ABCD的顶点A(-$\sqrt{3}$,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P的坐标为( )
如图,已知菱形ABCD的顶点A(-$\sqrt{3}$,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P的坐标为( )| A. | $({\frac{{3\sqrt{3}}}{4},-\frac{1}{4}})$ | B. | $({-\frac{{3\sqrt{3}}}{4},-\frac{1}{4}})$ | C. | $({-\sqrt{3},0})$ | D. | $({\sqrt{3},0})$ |
分析 先求出求出菱形的边长,再根据点P的运动速度求出沿A→B→C→D→A所需的时间,由 $\frac{2016}{16}$=126,推出移动到第2016秒和第16秒的位置相同,当P运动到第16秒时点P在点A处,推出移动到第2017秒时,点P在AB的$\frac{1}{4}$处,进而可得出结论.
解答 解:在Rt △AOD中,∵∠AOD=90°,∠DAO=30°,OA=$\sqrt{3}$,
△AOD中,∵∠AOD=90°,∠DAO=30°,OA=$\sqrt{3}$,
∴OD=1,AD=2OD=2,
∵点P的运动速度为0.5米/秒,
∴从点A到点B所需时间=$\frac{2}{0.5}$=4秒,
∴沿A→B→C→D→A所需的时间=4×4=16秒.
∵$\frac{2016}{16}$=126,
∴移动到第2016秒和第16秒的位置相同,当P运动到第16秒时点P在点A处,
∴移动到第2017秒时,点P在AB的$\frac{1}{4}$处,PA=$\frac{1}{4}$AB,此时P的坐标为(-$\frac{3\sqrt{3}}{4}$,-$\frac{1}{4}$).
故选B.
点评 本题考查的是菱形的性质、直角三角形30度角所对的直角边等于斜边的一半、勾股定理等知识,根据题意得出点P运动一周所需的时间是解答此题的关键,记住速度、时间、路程之间的关系,属于中考选择题中的压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列汽车标志中即是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.若关于x的一元二次方程x2+(k+3)x+2=0的一个根是-1,则另一个根是( )
| A. | 1 | B. | 0 | C. | 2 | D. | -2 |
8.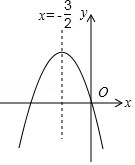 如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
①abc=0,②a+b+c>0,③a>b,④4ac-b2<0; 其中正确的结论有( )
 如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0; 其中正确的结论有( )
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
5.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a5 | C. | ${(\frac{1}{2})}^{-1}$=2 | D. | ${(\frac{1}{2})}^{0}$=0 |
2.在平面直角坐标系内,把抛物线y=(x-1)2+3向下平移2个单位,那么所得抛物线的解析式是( )
| A. | y=(x-3)2 | B. | y=(x+1)2 | C. | y=(x-1)2+5 | D. | y=(x-1)2+1 |
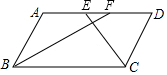 如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( )
如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( )