题目内容
8. 如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
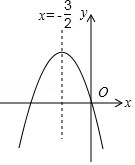
如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0; 其中正确的结论有( )
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
分析 首先根据二次函数y=ax2+bx+c的图象经过原点,可得c=0,所以abc=0;然后根据x=1时,y<0,可得a+b+c<0;再根据图象开口向下,可得a<0,图象的对称轴为x=-$\frac{b}{2a}$=-$\frac{3}{2}$,所以b=3a,a>b;最后根据二次函数y=ax2+bx+c图象与x轴有两个交点,可得△>0,所以b2-4ac>0,4ac-b2<0,据此解答即可
解答 解:∵二次函数y=ax2+bx+c图象经过原点,
∴c=0,
∴abc=0,故①正确;
∵x=1时,y<0,
∴a+b+c<0,故②不正确;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴是x=-$\frac{3}{2}$,
∴-$\frac{b}{2a}$=-$\frac{3}{2}$,
∴b=3a,
又∵a<0,b<0,
∴a>b,故③正确;
∵二次函数y=ax2+bx+c图象与x轴有两个交点,
∴△>0,
∴b2-4ac>0,4ac-b2<0,故④正确;
综上,可得正确结论有3个:①③④.
故选C.
点评 本题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
相关题目
18.已知一个圆锥的母线长是5,底面的半径是4,则这个圆锥的侧面积是( )
| A. | 20π | B. | 15π | C. | 12π | D. | 36π |
19.2017年4月8日,中国财经新闻报道中国3月外汇储备30090.9亿,这个数据用科学记数法表示为( )
| A. | 3.00909×104 | B. | 3.00909×105 | C. | 3.00909×1012 | D. | 3.00909×1013 |
16.有11名同学参加传统文化比赛,他们的预赛成绩各不相同,现取其中前5名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这11名同学成绩的( )
| A. | 方差 | B. | 平均数 | C. | 众数 | D. | 中位数 |
3.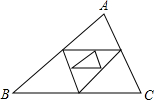 如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )
如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )
 如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )
如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
13.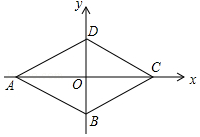 如图,已知菱形ABCD的顶点A(-$\sqrt{3}$,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P的坐标为( )
如图,已知菱形ABCD的顶点A(-$\sqrt{3}$,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P的坐标为( )
 如图,已知菱形ABCD的顶点A(-$\sqrt{3}$,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P的坐标为( )
如图,已知菱形ABCD的顶点A(-$\sqrt{3}$,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P的坐标为( )| A. | $({\frac{{3\sqrt{3}}}{4},-\frac{1}{4}})$ | B. | $({-\frac{{3\sqrt{3}}}{4},-\frac{1}{4}})$ | C. | $({-\sqrt{3},0})$ | D. | $({\sqrt{3},0})$ |
20.计算(3a-2b)2的结果为( )
| A. | 9a2+4b2 | B. | 9a2+6ab+4b2 | C. | 9a2-12ab+4b2 | D. | 9a2-4b2 |
17. 如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=40°,点D是弧BAC上一点,连结CD.则∠D的度数是( )
如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=40°,点D是弧BAC上一点,连结CD.则∠D的度数是( )
 如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=40°,点D是弧BAC上一点,连结CD.则∠D的度数是( )
如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=40°,点D是弧BAC上一点,连结CD.则∠D的度数是( )| A. | 50° | B. | 45° | C. | 40° | D. | 35° |
18.下列说法正确的是( )
| A. | 不可能事件发生的概率为1 | |
| B. | 随机事件发生的概率为$\frac{1}{3}$ | |
| C. | 概率很小的事件不可能发生 | |
| D. | 掷一枚质地均匀的硬币,正面朝上的概率为$\frac{1}{2}$ |