题目内容
3．计算：60°-9°25′=50°35′．分析 由1°=60′，计算60°-9°25′，即可得出结论．
解答 解：60°-9°25′=50°35′．
故答案为：50°35′．
点评 本题考查了度分秒的换算，牢记1°=60′是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
13．
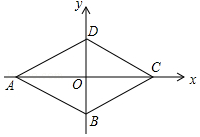如图，已知菱形ABCD的顶点A（-$\sqrt{3}$，0），∠DAB=60°，若动点P从点A出发，沿A→B→C→D→A→B→…的路径，在菱形的边上以每秒0.5个单位长度的速度移动，则第2017秒时，点P的坐标为（ ）
如图，已知菱形ABCD的顶点A（-$\sqrt{3}$，0），∠DAB=60°，若动点P从点A出发，沿A→B→C→D→A→B→…的路径，在菱形的边上以每秒0.5个单位长度的速度移动，则第2017秒时，点P的坐标为（ ）| A． | $（{\frac{{3\sqrt{3}}}{4}，-\frac{1}{4}}）$ | B． | $（{-\frac{{3\sqrt{3}}}{4}，-\frac{1}{4}}）$ | C． | $（{-\sqrt{3}，0}）$ | D． | $（{\sqrt{3}，0}）$ |
14．
一个几何体由若干大小相同的小立方块搭成，图分别是从它的正面、上面看到的形状图，则搭成该几何体的小立方块至少需要（ ）
一个几何体由若干大小相同的小立方块搭成，图分别是从它的正面、上面看到的形状图，则搭成该几何体的小立方块至少需要（ ）| A． | 5 块 | B． | 6 块 | C． | 7 块 | D． | 8 块 |
11．
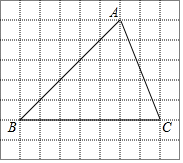在正方形网格中，△ABC的位置如图所示，则cos∠B的值为（ ）
在正方形网格中，△ABC的位置如图所示，则cos∠B的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
18．下列说法正确的是（ ）
| A． | 不可能事件发生的概率为1 | |
| B． | 随机事件发生的概率为$\frac{1}{3}$ | |
| C． | 概率很小的事件不可能发生 | |
| D． | 掷一枚质地均匀的硬币，正面朝上的概率为$\frac{1}{2}$ |
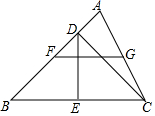如图，CD是△ABC的高，E，F，G分别是BC，AB，AC上的中点，求证：FG=DE．