题目内容
9.计算:$\sqrt{3}$($\sqrt{3}$+$\sqrt{27}$)=12.分析 先把$\sqrt{27}$化简,再本括号内合并,然后进行二次根式的乘法运算.
解答 解:原式=$\sqrt{3}$•($\sqrt{3}$+3$\sqrt{3}$)
=$\sqrt{3}$×4$\sqrt{3}$
=12.
故答案为12.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
19.2016的倒数是( )
| A. | $\frac{1}{2016}$ | B. | -$\frac{1}{2016}$ | C. | 2016 | D. | -2016 |
20.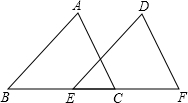 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )| A. | ∠A=∠D | B. | BC=EF | C. | ∠ACB=∠F | D. | AC=DF |
4.计算:20•2-3=( )
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | 0 | D. | 8 |
1.不等式组$\left\{\begin{array}{l}{x-1≤2-2x}\\{\frac{2x}{3}>\frac{x-1}{2}}\end{array}\right.$的解集是-3<x≤1.
4.在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球,这三个小球除颜色外其余都相同,若分别从两个口袋中随机取出一个小球,则取出的两个小球颜色相同的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
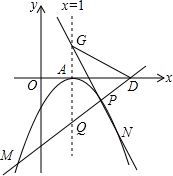 如图,已知直线y=kx+b(k>0)交抛物线y=-(x-1)2交于M、P两点,交抛物线对称轴x=1于Q(Q在x轴下方),交x轴于D,点N是点M关于对称轴x=1的对称点,延长NP交对称轴x=1于G,求证:DG=DQ.
如图,已知直线y=kx+b(k>0)交抛物线y=-(x-1)2交于M、P两点,交抛物线对称轴x=1于Q(Q在x轴下方),交x轴于D,点N是点M关于对称轴x=1的对称点,延长NP交对称轴x=1于G,求证:DG=DQ.