题目内容
2.关于x的一元二次方程kx2-(2k-2)x+(k-2)=0(k≠0).(1)求证:无论k取何值时,方程总有两个不相等的实数根.
(2)当k取何整数时方程有整数根.
分析 (1)根据一元二次方程的定义得k≠0,再计算判别式得到△=(2k-2)2-4k×(k-2)>0,然后根据非负数的性质即k的取值得到△>0,则可根据判别式的意义得到结论,;
(2)利用公式法表示出方程的两个根,再进一步理由方程有整数根探讨得出k的数值即可.
解答 (1)证明:这∵a=k,b=-(2k-2),c=k-2,
∴△=b2-4ac=[-(2k-2)]2-4k×(k-2)=4k2-8k+4-4k2+8k=4>0,
∴无论k取何值时,方程总有两个不相等的实数根.
(2)解:方程kx2-(2k-2)x+(k-2)=0(k≠0)的解为:$x=\frac{{-b±\sqrt{{b^2}-4ac}}}{2a}=\frac{{2k-2±\sqrt{4}}}{2k}$
整理,得${x_1}=1,{x_2}=\frac{k-2}{k}$
在方程的两个根中,x1=1是整数,
∴${x_2}=\frac{k-2}{k}$为整数,${x_2}=\frac{k-2}{k}=1-\frac{2}{k}$,
∵k为整数,
∴当k为±1和±2时方程有整数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
相关题目
13.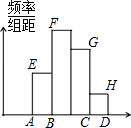 某校七年级在“数学小论文”评比活动中,共征集到论文30篇,并对其进行评比、整理,分成组画出频数分布直方图(如图),从左到右各小长方形的高度比为2:4:3:1,则第2组的频数为( )
某校七年级在“数学小论文”评比活动中,共征集到论文30篇,并对其进行评比、整理,分成组画出频数分布直方图(如图),从左到右各小长方形的高度比为2:4:3:1,则第2组的频数为( )
 某校七年级在“数学小论文”评比活动中,共征集到论文30篇,并对其进行评比、整理,分成组画出频数分布直方图(如图),从左到右各小长方形的高度比为2:4:3:1,则第2组的频数为( )
某校七年级在“数学小论文”评比活动中,共征集到论文30篇,并对其进行评比、整理,分成组画出频数分布直方图(如图),从左到右各小长方形的高度比为2:4:3:1,则第2组的频数为( )| A. | 12 | B. | 10 | C. | 9 | D. | 6 |
11.学校准备用一笔钱买奖品,若以1支钢笔和2本日记本为一份奖品,则可购买80份奖品,若以一支钢笔和4本日记本为一份奖品,则可购买60份奖品,问若以1支钢笔和1本日记本为一份奖品,则可购买96份奖品.
19.在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD.如果再增加条件AC=BD,此四边形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 都有可能 |