题目内容
14.若a,b为有理数,且$\sqrt{8}$×$\sqrt{18}$+$\sqrt{\frac{1}{8}}$=a+b$\sqrt{2}$,则ab=3.分析 先把各二次根式化为最简二次根式,再移项合并得到a-12+(b-$\frac{1}{4}$)×$\sqrt{2}$=0,由于a,b为有理数,根据实数运算得到a-12=0,b-$\frac{1}{4}$=0,解得a=12,b=$\frac{1}{4}$,然后计算ab的值.
解答 解:∵$\sqrt{8}$×$\sqrt{18}$+$\sqrt{\frac{1}{8}}$=a+b$\sqrt{2}$,
∴2$\sqrt{2}$×3$\sqrt{2}$+$\frac{\sqrt{2}}{4}$=a+b$\sqrt{2}$,
∴12+$\frac{\sqrt{2}}{4}$=a+b$\sqrt{2}$,
∴a-12+(b-$\frac{1}{4}$)×$\sqrt{2}$=0,
∵a,b为有理数,
∴a-12=0,b-$\frac{1}{4}$=0,解得a=12,b=$\frac{1}{4}$,
∴ab=12×$\frac{1}{4}$=3.
故答案为3.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
9.一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
 如图,数轴上A、B两点表示的数分别为1和$\sqrt{3}$,且AB=AC,那么数轴上C点表示的数为2-$\sqrt{3}$.
如图,数轴上A、B两点表示的数分别为1和$\sqrt{3}$,且AB=AC,那么数轴上C点表示的数为2-$\sqrt{3}$.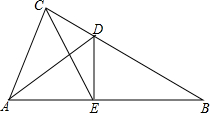 如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.
如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.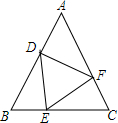 已知,如图,△ABC中,AB=AC,动点D、E、F在AB、BC、AC上移动,移动过程中始终保持BD=CE,∠DEF=∠B,请你分析是否存在始终与△BDE全等的三角形,并说明理由.
已知,如图,△ABC中,AB=AC,动点D、E、F在AB、BC、AC上移动,移动过程中始终保持BD=CE,∠DEF=∠B,请你分析是否存在始终与△BDE全等的三角形,并说明理由.