Question

16．已知：点D、E、F分别是三角形ABC的边BC、CA、AB上的点，DE∥，DF∥CA．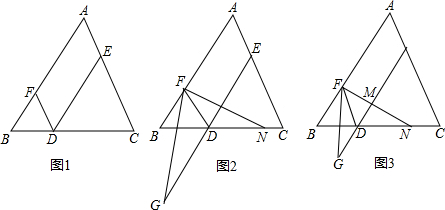

（1）如图1，求证：∠FDE=∠A．
（2）如图2，点G为线段ED延长线上一点，连接FG，∠AFG的平分线FN交DE于点M，交BC于点N．请直接写出∠AFG、∠B、∠BNF的数量关系是∠B+∠BNF=$\frac{1}{2}$∠AFG．
（3）如图3，在（2）的条件下，若FG恰好平分∠BFD，∠BNF=20°，且∠FDE-∠B=5°，求∠A的度数．

Answer 1

分析 （1）根据平行线的性质进行证明即可；
（2）根据（1）中得出即可；
（3）根据三角形的内角和定理进行解答即可．

解答 （1）证明：∵DE∥BA，
∴∠A+∠AFD=180°，
∵DF∥CA，
∴∠FDE+∠AFD=180°，
∴∠FDE=∠A，
（2）解：∠B+∠BNF=$\frac{1}{2}$∠AFG；
（3）解：设∠BFG=x，
则∠AFG=180°-x，
∵FG平分∠BFD，
∴∠BFD=2∠BFG=2x，
∵DF∥CA，
∴∠FDE=∠A=∠BFD=2x，
∵∠FDE-∠B=5°，
∴∠B=2x-5°，
∵∠BNF=20°，
∴2x-5°+20°=$\frac{1}{2}$（180°-x）
∴x=30°，
∴∠A=2x=60°，

点评 此题考查三角形的内角和问题，关键是根据平行线的性质和三角形的内角和定理进行解答．