题目内容
 家乐超市老板到批发中心选购甲、乙两种品牌的文具用品.乙品牌文具用品的进货单价是甲品牌文具用品进货单价的2倍,考虑各种因素,预计购进乙品牌文具用品的数量y(个)与甲品牌文具用品的数量x(个)之间的函数关系为y=-x+b,函数图象如图.当购进的甲、乙品牌的文具用品中,甲有120个时,购进甲、乙品牌文具用品共需7200元.
家乐超市老板到批发中心选购甲、乙两种品牌的文具用品.乙品牌文具用品的进货单价是甲品牌文具用品进货单价的2倍,考虑各种因素,预计购进乙品牌文具用品的数量y(个)与甲品牌文具用品的数量x(个)之间的函数关系为y=-x+b,函数图象如图.当购进的甲、乙品牌的文具用品中,甲有120个时,购进甲、乙品牌文具用品共需7200元.(1)求y与x之间的函数关系式;
(2)求a的值是多少?
(3)求甲、乙两种品牌文具用品的进货单价.
考点:一次函数的应用
专题:
分析:(1)由函数图象将x=50,y=250时代入y=-x+b求出b的值即可;
(2)把坐标(a,100)代入(1)的解析式就可以求出a的值得出结论;
(3)当y=120时代入(1)的解析式就可以求出x的值,设甲品牌文具用品进货单价为m元,则乙品牌文具用品的进货单价为2m元,根据甲、乙品牌文具用品共需7200元建立方程求出其解即可.
(2)把坐标(a,100)代入(1)的解析式就可以求出a的值得出结论;
(3)当y=120时代入(1)的解析式就可以求出x的值,设甲品牌文具用品进货单价为m元,则乙品牌文具用品的进货单价为2m元,根据甲、乙品牌文具用品共需7200元建立方程求出其解即可.
解答:解:91)由题意,得
250=-50+b,
b=300.
y与x之间的函数关系式为:y=-x+300;
(2)由题意,得
100=-a+300,
a=200.
答:a=200;
(3)当x=120时,y=-120+300,
y=180.
设甲品牌文具用品进货单价为m元,则乙品牌文具用品的进货单价为2m元,由题意,得
120m+180×2m=7200,
解得:m=15,
∴乙品牌文具用品的进货单价为30元.
答:甲品牌文具用品进货单价为15元,乙品牌文具用品的进货单价为30元.
250=-50+b,
b=300.
y与x之间的函数关系式为:y=-x+300;
(2)由题意,得
100=-a+300,
a=200.
答:a=200;
(3)当x=120时,y=-120+300,
y=180.
设甲品牌文具用品进货单价为m元,则乙品牌文具用品的进货单价为2m元,由题意,得
120m+180×2m=7200,
解得:m=15,
∴乙品牌文具用品的进货单价为30元.
答:甲品牌文具用品进货单价为15元,乙品牌文具用品的进货单价为30元.
点评:本题考查了一次函数的解析式的运用,待定系数法求一次函数的解析式的运用,列一元一次方程进而实际问题的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列方程中,解是x=2的方程是( )
| A、3x=x+3 |
| B、-x+3=0 |
| C、5x-2=8 |
| D、2x=6 |
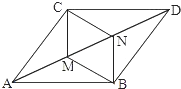 如图,?ABDC中,BN⊥AB,交AD于点N,CM⊥CD,交AD于点M,连接BM、CN
如图,?ABDC中,BN⊥AB,交AD于点N,CM⊥CD,交AD于点M,连接BM、CN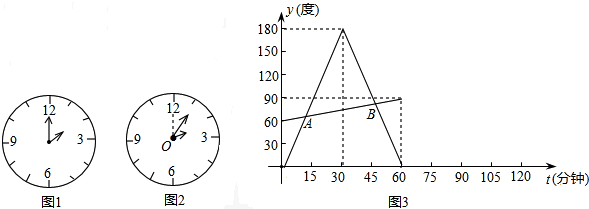
 已知:如图,∠D=110°,∠EFD=70°,∠1=∠2.求证:∠3=∠B.
已知:如图,∠D=110°,∠EFD=70°,∠1=∠2.求证:∠3=∠B.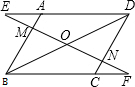 已知:如图在平行四边形ABCD中,对角线BD的中点为O,过点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
已知:如图在平行四边形ABCD中,对角线BD的中点为O,过点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F. 如图,在△ABC中,∠A=α,∠ABC的平分线与△ABC的外角∠ACD的平分线交于点A1,得∠A1=
如图,在△ABC中,∠A=α,∠ABC的平分线与△ABC的外角∠ACD的平分线交于点A1,得∠A1=