Question

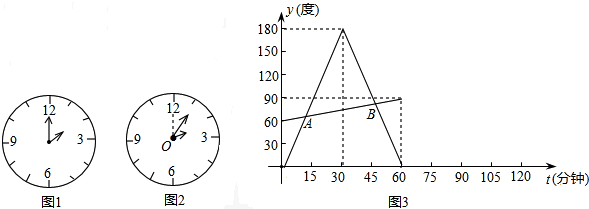
小华观察钟面（图1），了解到钟面上的分针每小时旋转360度，时针每小时旋转30度．他为了进一步探究钟面上分针与时针的旋转规律，从下午2：00开始对钟面进行了一个小时的观察，为了探究方便，他将分针与时针起始位置OP（图2）的夹角记为y₁，时针与OP的夹角记为y₂度（夹角是指不大于平角的角），旋转时间记为t分钟，观察结束后，他利用活动的数据绘制成图象（图3），并求出y₁与t的函数关系式：
y₁=

6t       (0≤t≤30) -6t+360   (30＜t≤60)

请完成：
（1）分针由起始位置12运动到6（旋转了180°），则时针旋转了多少度？
（2）求出图3中y₃与t的函数关系式；
（3）直接写出A、B两点的坐标，并解释这两点的实际意义．

Answer 1

考点：几何变换综合题

专题：

分析：（1）根据时针每小时旋转30度，则

1

2

小时旋转15°；
（2）设y₂与t的函数关系式为y₂=kt+b，再把（0，60），（60，90）代入此函数关系式即可求出k、b的值，进而得出结论；
（3）求出两个函数的交点坐标即可；

解答：解：（1）时针旋转的度数=30×

1

2

=15（度）；

（2）设y₂与t的函数关系式为y₂=kt+b，再把（0，60），（60，90）代入得：

60=b 90=60k+b

，解得

b=60 k=0.5

，
则解析式是：y=0.5t+60．
故y₂与t的函数关系式为y₂=0.5t+60．

（3）A（

120

11

，

720

11

），B（

600

13

，

1080

13

）；
当0≤t≤30时，则

y1=6t y2=0.5t+60

，
解得

t= 120 11 y= 720 11

，
所以A（

120

11

，

720

11

）；
当30＜t≤60时，则

y1=-6t+360 y2=0.5t+60

，
解得

t= 600 13 y= 1080 13

，
所以B（

600

13

，

1080

13

）；
故A（

120

11

，

720

11

），B（

600

13

，

1080

13

）；
A表示时针与分针第一次重合的情况，B表示是经过

600

13

分钟时针与分针关于OP成轴对称且与OP的夹角为

1080

13

．

点评：本题主要考查了一次函数的图象和交点坐标的求解，正确理解分针与时针转动的情况是解题的关键．