题目内容
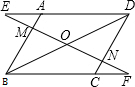 已知:如图在平行四边形ABCD中,对角线BD的中点为O,过点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
已知:如图在平行四边形ABCD中,对角线BD的中点为O,过点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.(1)证明:OE=OF;
(2)若连接BE,DF,判断四边形BFDE的形状(简述理由);
(3)若将直线EF绕O点旋转(EF不重合于BD),四边形BFDE的形状如何?若四边形BFDE为矩形,则∠DOF与∠DBF满足怎样的数量关系(直接给出结论即可).
考点:平行四边形的判定与性质,全等三角形的判定与性质,矩形的性质
专题:
分析:(1)证明△DOE≌△BOF,根据全等三角形的对应边相等即可证得;
(2)根据对角线互相平分的四边形是平行四边形即可判断;
(3)根据对角线互相平分的四边形是平行四边形即可判断四边形BFDE的形状,根据矩形的性质:对角线相等,求得OB=OF,根据等边对等角得出∠OBF=∠OFB,最后根据三角形的外角的性质即可求得;
(2)根据对角线互相平分的四边形是平行四边形即可判断;
(3)根据对角线互相平分的四边形是平行四边形即可判断四边形BFDE的形状,根据矩形的性质:对角线相等,求得OB=OF,根据等边对等角得出∠OBF=∠OFB,最后根据三角形的外角的性质即可求得;
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EDO=∠FBO,∠E=∠F.
在△DOE与△BOF中,
,
∴△DOE≌△BOF(AAS)
∴OE=OF;
(2)四边形BFDE为平行四边形.
∵OD=OB,OE=OF
∴四边形BFDE为平行四边形.
(3)将直线EF绕O点旋转,四边形BFDE仍为平行四边形.
若四边形BFDE为矩形,则∠DOF=2∠DBF.
理由:∵OD=OB,OE=OF,
∴四边形BFDE为平行四边形;
∵若四边形BFDE为矩形,则EF=BD,
∴OB=OF,
∴∠OBF=∠OFB,
∵∠DOF=∠OBF+∠OFB,
∴∠DOF=2∠DBF;
∴AD∥BC.
∴∠EDO=∠FBO,∠E=∠F.
在△DOE与△BOF中,
|
∴△DOE≌△BOF(AAS)
∴OE=OF;
(2)四边形BFDE为平行四边形.
∵OD=OB,OE=OF
∴四边形BFDE为平行四边形.
(3)将直线EF绕O点旋转,四边形BFDE仍为平行四边形.
若四边形BFDE为矩形,则∠DOF=2∠DBF.
理由:∵OD=OB,OE=OF,
∴四边形BFDE为平行四边形;
∵若四边形BFDE为矩形,则EF=BD,
∴OB=OF,
∴∠OBF=∠OFB,
∵∠DOF=∠OBF+∠OFB,
∴∠DOF=2∠DBF;
点评:本题考查了平行四边形的性质、三角形全等的判定和性质、矩形的性质等,本题的关键是熟练掌握平行四边形的判定定理和性质定理,以及矩形的性质定理;

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 点M是正方形ABCD的边AB的中点,连接DM,将△ADM沿DM翻折得△A′DM,延长MA′交DC的延长线于点E,求
点M是正方形ABCD的边AB的中点,连接DM,将△ADM沿DM翻折得△A′DM,延长MA′交DC的延长线于点E,求 家乐超市老板到批发中心选购甲、乙两种品牌的文具用品.乙品牌文具用品的进货单价是甲品牌文具用品进货单价的2倍,考虑各种因素,预计购进乙品牌文具用品的数量y(个)与甲品牌文具用品的数量x(个)之间的函数关系为y=-x+b,函数图象如图.当购进的甲、乙品牌的文具用品中,甲有120个时,购进甲、乙品牌文具用品共需7200元.
家乐超市老板到批发中心选购甲、乙两种品牌的文具用品.乙品牌文具用品的进货单价是甲品牌文具用品进货单价的2倍,考虑各种因素,预计购进乙品牌文具用品的数量y(个)与甲品牌文具用品的数量x(个)之间的函数关系为y=-x+b,函数图象如图.当购进的甲、乙品牌的文具用品中,甲有120个时,购进甲、乙品牌文具用品共需7200元. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后.△ABC的顶点均在格点上.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后.△ABC的顶点均在格点上.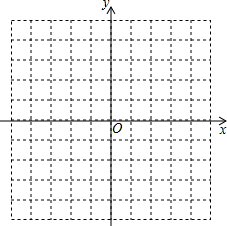 已知:在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).
已知:在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).