题目内容
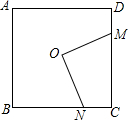 如图,点O是边长为a的正方形ABCD的对称中心,过点作OM⊥ON交正方形的边于M、N两点,求四边形OMCN的面积.
如图,点O是边长为a的正方形ABCD的对称中心,过点作OM⊥ON交正方形的边于M、N两点,求四边形OMCN的面积.考点:旋转的性质,正方形的性质
专题:
分析:连接OC、OD,根据正方形的性质可得OC=OD,∠COD=90°,∠OCD=∠ODC=45°,根据同角的余角相等求出∠CON=∠DOM,然后利用“角边角”证明△CON和△DOM全等,根据全等三角形的面积相等可得S△CON=S△DOM,从而求出S四边形OMCN=S△COD,然后根据正方形的性质求解即可.
解答: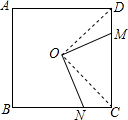 解:如图,连接OC、OD,
解:如图,连接OC、OD,
∵四边形ABCD是正方形,
∴OC=OD,∠COD=90°,∠OCD=∠ODC=45°,
∴∠DOM+∠COM=90°,
∵OM⊥ON,
∴∠CON+∠COM=90°,
∴∠CON=∠DOM,
在△CON和△DOM中,
,
∴△CON≌△DOM(ASA),
∴S△CON=S△DOM,
∴S四边形OMCN=S△COD,
∵正方形ABCD的边长为a,
∴S△COD=
a2,
∴四边形OMCN的面积为
a2.
 解:如图,连接OC、OD,
解:如图,连接OC、OD,∵四边形ABCD是正方形,
∴OC=OD,∠COD=90°,∠OCD=∠ODC=45°,
∴∠DOM+∠COM=90°,
∵OM⊥ON,
∴∠CON+∠COM=90°,
∴∠CON=∠DOM,
在△CON和△DOM中,
|
∴△CON≌△DOM(ASA),
∴S△CON=S△DOM,
∴S四边形OMCN=S△COD,
∵正方形ABCD的边长为a,
∴S△COD=
| 1 |
| 4 |
∴四边形OMCN的面积为
| 1 |
| 4 |
点评:本题考查了旋转的性质,正方形的性质,全等三角形的判定与性质,作辅助线构造出全等三角形并求出S四边形OMCN=S△COD是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 某销售公司出售某种产品,满足下列条件:
某销售公司出售某种产品,满足下列条件: 如图,点E是?ABCD边AD上一点,且AE=
如图,点E是?ABCD边AD上一点,且AE=