题目内容
已知方程(a-x)2=a(x2+x+a)-8a+16是关于x的一元二次方程.
(1)求a的取值范围;
(2)若该方程的一次项系数为0,求此方程的根.
(1)求a的取值范围;
(2)若该方程的一次项系数为0,求此方程的根.
考点:一元二次方程的定义,一元二次方程的一般形式
专题:
分析:(1)一元二次方程的二次项系数不为零;
(2)先把原方程转化为一般式方程,然后找到一次项系数,根据“该方程的一次项系数为0”求得a的值;然后解方程.
(2)先把原方程转化为一般式方程,然后找到一次项系数,根据“该方程的一次项系数为0”求得a的值;然后解方程.
解答:解:(1)化简,得
(a-1)x2+3ax-8a+16=0.
方程(a-x)2=a(x2+x+a)-8a+16是关于x的一元二次方程,得
a-1≠0,解得a≠1,
当a≠1时,方程(a-x)2=a(x2+x+a)-8a+16是关于x的一元二次方程;
(2)由一次项系数为零,得a=0.
原方程是-x2+16=0,即x2-16=0.
因式分解得(x+4)(x-4)=0,
解得x1=-4,x2=4.
(a-1)x2+3ax-8a+16=0.
方程(a-x)2=a(x2+x+a)-8a+16是关于x的一元二次方程,得
a-1≠0,解得a≠1,
当a≠1时,方程(a-x)2=a(x2+x+a)-8a+16是关于x的一元二次方程;
(2)由一次项系数为零,得a=0.
原方程是-x2+16=0,即x2-16=0.
因式分解得(x+4)(x-4)=0,
解得x1=-4,x2=4.
点评:本题考查了一元二次方程的定义,一元二次方程的二次项的系数不能为零,一元二次方程不含一次项时可选因式分解法解一元二次方程.

练习册系列答案
相关题目
已知二次函数y=x2-4x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-4x+m=0的两个实数根是( )
| A、x1=1,x2=-1 |
| B、x1=-1,x2=2 |
| C、x1=-1,x2=0 |
| D、x1=1,x2=3 |
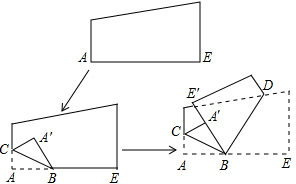 如图是一张边被裁直的白纸,把一边折叠后,BC、BD为折痕,A′、E′、B在同一直线上,则∠CBD的度数( )
如图是一张边被裁直的白纸,把一边折叠后,BC、BD为折痕,A′、E′、B在同一直线上,则∠CBD的度数( )| A、不能确定 | B、大于90° |
| C、小于90° | D、等于90° |
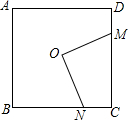 如图,点O是边长为a的正方形ABCD的对称中心,过点作OM⊥ON交正方形的边于M、N两点,求四边形OMCN的面积.
如图,点O是边长为a的正方形ABCD的对称中心,过点作OM⊥ON交正方形的边于M、N两点,求四边形OMCN的面积. 在图中共有
在图中共有