题目内容
如图,△ABC是等边三角形,点M是BC上任意一点,点N是CA上任意一点,且BM=CN,直线BN与AM相交于点Q,就下面给出的两种情况,猜测∠BQM等于多少度,并利用图②说明结论的正确性.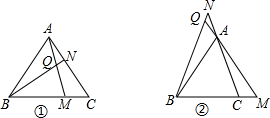
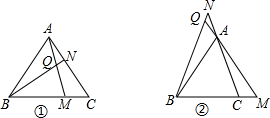
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据等边三角形的性质得出AB=AC,∠ABC=∠BCA=∠ACB=60°,根据SAS推出△ABM≌△BCN,根据全等得出∠M=∠N,求出∠BQM=∠N+∠NAQ=∠ACB,即可得出答案.
解答:解:∠BQM=60°
∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠BCA=∠ACB=60°,
在△ABM和△BCN中
∴△ABM≌△BCN(SAS),
∴∠M=∠N,
又∠NAQ=∠MAC,
∴∠BQM=∠N+∠NAQ=∠M+∠MAC=∠ACB=60°.
∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠BCA=∠ACB=60°,
在△ABM和△BCN中
|
∴△ABM≌△BCN(SAS),
∴∠M=∠N,
又∠NAQ=∠MAC,
∴∠BQM=∠N+∠NAQ=∠M+∠MAC=∠ACB=60°.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
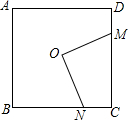 如图,点O是边长为a的正方形ABCD的对称中心,过点作OM⊥ON交正方形的边于M、N两点,求四边形OMCN的面积.
如图,点O是边长为a的正方形ABCD的对称中心,过点作OM⊥ON交正方形的边于M、N两点,求四边形OMCN的面积. 二次函数y=ax2+bx+c的图象如图所示,则下列结论:
二次函数y=ax2+bx+c的图象如图所示,则下列结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,请结合图象,判断下列各式的符号.①abc;②b2-4ac;③a+b+c;④a-b+c.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,请结合图象,判断下列各式的符号.①abc;②b2-4ac;③a+b+c;④a-b+c. 在图中共有
在图中共有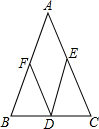 如图,在△ABC中,点D在BC上,DE∥AB交AC于点E,DF∥AC交AB于点F,且BC=5,
如图,在△ABC中,点D在BC上,DE∥AB交AC于点E,DF∥AC交AB于点F,且BC=5,