题目内容
 如图,点E是?ABCD边AD上一点,且AE=
如图,点E是?ABCD边AD上一点,且AE=| 1 |
| 2 |
(1)AB=2AF;
(2)S△CED=8S△AOE;
(3)3S△CED=4S△AFC.
考点:平行四边形的性质
专题:证明题
分析:(1)利用平行线分线段成比例定理得出
=
=
,进而得出答案;
(2)利用三角形面积关系以及相似三角形的性质得出即可;
(3)利用同一未知数表示出各三角形面积进而得出答案.
| AF |
| BF |
| AE |
| BC |
| 1 |
| 3 |
(2)利用三角形面积关系以及相似三角形的性质得出即可;
(3)利用同一未知数表示出各三角形面积进而得出答案.
解答: 证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AE=
ED,
∴AE=
BC,
∴
=
=
,
∴
=
,
∴AB=2AF;
(2)∵AE=
ED,
∴S△AEC:S△CDE=1:2,
∵AE∥BC,
∴△AOE∽△COB,
∵
=
=
,
∴
=
,
∴
=
,
∴S△CED=8S△AOE;
(3)∵由(1)得
=
,
∴
=
,
设S△FAE=x,则S△AEC=2x,
∵AE=
ED,
∴S△AEC=
S△CDE,
∴S△CDE=4x,
∴3S△CED=4S△AFC.
 证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,
∵AE=
| 1 |
| 2 |
∴AE=
| 1 |
| 3 |
∴
| AF |
| BF |
| AE |
| BC |
| 1 |
| 3 |
∴
| AF |
| AB |
| 1 |
| 2 |
∴AB=2AF;
(2)∵AE=
| 1 |
| 2 |
∴S△AEC:S△CDE=1:2,
∵AE∥BC,
∴△AOE∽△COB,
∵
| AE |
| BC |
| AO |
| CO |
| 1 |
| 3 |
∴
| S△AOE |
| S△EOC |
| 1 |
| 3 |
∴
| S△AOE |
| S△AEC |
| 1 |
| 4 |
∴S△CED=8S△AOE;
(3)∵由(1)得
| AF |
| AB |
| 1 |
| 2 |
∴
| S△FAE |
| S△AEC |
| 1 |
| 2 |
设S△FAE=x,则S△AEC=2x,
∵AE=
| 1 |
| 2 |
∴S△AEC=
| 1 |
| 2 |
∴S△CDE=4x,
∴3S△CED=4S△AFC.
点评:此题主要考查了平行四边形的性质以及相似三角形的判定与性质,熟练利用三角形边的关系得出面积关系是解题关键.

练习册系列答案
相关题目
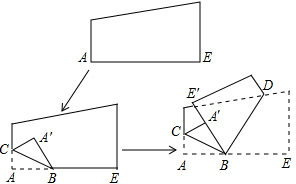 如图是一张边被裁直的白纸,把一边折叠后,BC、BD为折痕,A′、E′、B在同一直线上,则∠CBD的度数( )
如图是一张边被裁直的白纸,把一边折叠后,BC、BD为折痕,A′、E′、B在同一直线上,则∠CBD的度数( )| A、不能确定 | B、大于90° |
| C、小于90° | D、等于90° |
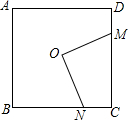 如图,点O是边长为a的正方形ABCD的对称中心,过点作OM⊥ON交正方形的边于M、N两点,求四边形OMCN的面积.
如图,点O是边长为a的正方形ABCD的对称中心,过点作OM⊥ON交正方形的边于M、N两点,求四边形OMCN的面积.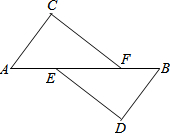 已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠D,AC∥BD,
已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠D,AC∥BD, 二次函数y=ax2+bx+c的图象如图所示,则下列结论:
二次函数y=ax2+bx+c的图象如图所示,则下列结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,请结合图象,判断下列各式的符号.①abc;②b2-4ac;③a+b+c;④a-b+c.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,请结合图象,判断下列各式的符号.①abc;②b2-4ac;③a+b+c;④a-b+c. 在图中共有
在图中共有