题目内容
10. 如图,半径为2的⊙O与正五边形ABCDE的两边AE、CD相切于点A、C,则劣弧$\widehat{AC}$长度为( )
如图,半径为2的⊙O与正五边形ABCDE的两边AE、CD相切于点A、C,则劣弧$\widehat{AC}$长度为( )| A. | $\frac{3}{5}$π | B. | $\frac{4}{5}$π | C. | $\frac{8}{5}$π | D. | $\frac{2}{3}$π |
分析 连接OA、OC,根据切线的性质得到∠OAE=90°,∠OCD=90°,根据正多边形的内角和公式求出正五边形的内角的度数,求出∠AOC的度数,利用弧长公式计算即可.
解答 解: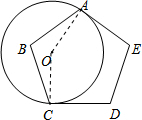 连接OA、OC,
连接OA、OC,
∵AE、CD切⊙O于点A、C,
∴∠OAE=90°,∠OCD=90°,
正五边形ABCDE的每个内角的度数为$\frac{(5-2)×180°}{5}$=108°,
∴∠AOC=540°-90°-90°-108°-108°=144°,
∴$\widehat{AC}$长度=$\frac{144π×2}{180}$=$\frac{8}{5}π$,
故选:C.
点评 本题考查的是弧长的计算和正多边形的内角和公式的应用,掌握弧长的计算公式:l=$\frac{nπr}{180}$是解题的关键.

练习册系列答案
相关题目
20.若|a+3|=6,则数轴上有理数a对应的点与-2对应的点的距离是( )
| A. | 3 | B. | 11 | C. | 5或11 | D. | 5或7 |
2.如果分式$\frac{x-2}{x+3}$的值为零,那么x的值是( )
| A. | x=2 | B. | x=-3 | C. | x=-2 | D. | x=3 |
 如图,点C,D在线段BF上,AB∥DE,AB=DF,∠A=∠F.求证:△ABC≌△FDE.
如图,点C,D在线段BF上,AB∥DE,AB=DF,∠A=∠F.求证:△ABC≌△FDE. 如图,DE⊥EB于点E,∠1=∠C,∠2与∠C互为余角,判断DE与BC是否平行,并说明理由.
如图,DE⊥EB于点E,∠1=∠C,∠2与∠C互为余角,判断DE与BC是否平行,并说明理由.