题目内容
17.解方程:(1)3x2-$\sqrt{2}$x-2=0;
(2)7x(5x+2)=6(5x+2)
分析 (1)求出b2-4ac的值,再代入公式求出即可;
(2)移项,分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)3x2-$\sqrt{2}$x-2=0,
b2-4ac=(-$\sqrt{2}$)2-4×3×(-2)=26,
x=$\frac{\sqrt{2}±\sqrt{26}}{2×3}$,
x1=$\frac{\sqrt{2}+\sqrt{26}}{6}$,x2=$\frac{\sqrt{2}-\sqrt{6}}{6}$;
(2)7x(5x+2)=6(5x+2),
7x(5x+2)-6(5x+2)=0,
(5x+2)(7x-6)=0,
5x+2=0,7x-6=0,
x1=-$\frac{2}{5}$,x2=$\frac{6}{7}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
相关题目
7. 如图,小波在周末时随父母到郊外放风筝,已知风筝线与水平线的夹角为45°,他放出的风筝线长是30m,此时,他手距地面1.5米,你认为能否算出此时风筝的高度?若能,请你帮他算一算;若不能,请说明理由.
如图,小波在周末时随父母到郊外放风筝,已知风筝线与水平线的夹角为45°,他放出的风筝线长是30m,此时,他手距地面1.5米,你认为能否算出此时风筝的高度?若能,请你帮他算一算;若不能,请说明理由.
 如图,小波在周末时随父母到郊外放风筝,已知风筝线与水平线的夹角为45°,他放出的风筝线长是30m,此时,他手距地面1.5米,你认为能否算出此时风筝的高度?若能,请你帮他算一算;若不能,请说明理由.
如图,小波在周末时随父母到郊外放风筝,已知风筝线与水平线的夹角为45°,他放出的风筝线长是30m,此时,他手距地面1.5米,你认为能否算出此时风筝的高度?若能,请你帮他算一算;若不能,请说明理由.
5. 如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )
如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )
 如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )
如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )| A. | ∠BEC=∠BFO | B. | ∠BEC+∠BFO=135° | C. | $\frac{1}{2}$∠BEC+∠BFO=90° | D. | ∠BEC+$\frac{1}{2}$∠BFO=90° |
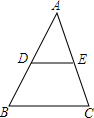 如图,已知$\frac{AD}{DB}=\frac{AE}{EC}=\frac{3}{2}$,求$\frac{AB}{DB}$,$\frac{EC}{AC}$,$\frac{AB}{AD}$.
如图,已知$\frac{AD}{DB}=\frac{AE}{EC}=\frac{3}{2}$,求$\frac{AB}{DB}$,$\frac{EC}{AC}$,$\frac{AB}{AD}$.