题目内容
设p,q都是实数,且p<q.我们规定:满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间,表示为[p,q].对于一个函数,如果它的自变量x与函数值y满足:当p≤x≤q时,有p≤y≤q,我们就称此函数是闭区间[p,q]上的“闭函数”.
(1)反比例函数y=
是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若实数c,d满足c<d,且d>2,当二次函数y=
x2-2x是闭区间[c,d]上的“闭函数”时,求c,d的值.
(1)反比例函数y=
| 2014 |
| x |
(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若实数c,d满足c<d,且d>2,当二次函数y=
| 1 |
| 2 |
考点:二次函数的性质,一次函数的性质,反比例函数的性质
专题:新定义
分析:(1)根据反比例函数y=
的单调区间进行判断;
(2)根据新定义运算法则列出关于系数k、b的方程组
或
,通过解该方程组即可求得系数k、b的值;
(3)y=
x2-2x=
(x2-4x+4)-2=
(x-2)2-2,所以该二次函数的图象开口方向向上,最小值是-2,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.由于c<d,且d>2,所以分两种情况进行讨论:①c<2<d;②c≥2.
| 2014 |
| x |
(2)根据新定义运算法则列出关于系数k、b的方程组
|
|
(3)y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)反比例函数y=
是闭区间[1,2014]上的“闭函数”,理由如下:
反比例函数y=
在第一象限,y随x的增大而减小,
当x=1时,y=2014;
当x=2014时,y=1,
所以,当1≤x≤2014时,有1≤y≤2014,符合闭函数的定义,故
反比例函数y=
是闭区间[1,2014]上的“闭函数”;
(2)分两种情况:k>0或k<0.
①当k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,故根据“闭函数”的定义知,
,
解得
.
∴此函数的解析式是y=x;
②当k<0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而减小,故根据“闭函数”的定义知,
,
解得
.
∴此函数的解析式是y=-x+m+n;
(3)∵y=
x2-2x=
(x2-4x+4)-2=
(x-2)2-2,
∴该二次函数的图象开口方向向上,最小值是-2,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.
①当c<2<d时,此时二次函数y=
x2-2x的最小值是-2=c,根据“闭函数”的定义知,
d=
c2-2c或d=
d2-2d;
Ⅰ)当d=
c2-2c时,由于d=
×(-2)2-2×(-2)=6>2,符合题意;
Ⅱ)当d=
d2-2d时,解得d=0或6,
由于d>2,
所以d=6;
②当c≥2时,此二次函数y随x的增大而增大,则根据“闭函数”的定义知,
,
解得,
,
∵c<d,
∴
不合题意,舍去.
综上所述,c,d的值分别为-2,6.
| 2014 |
| x |
反比例函数y=
| 2014 |
| x |
当x=1时,y=2014;
当x=2014时,y=1,
所以,当1≤x≤2014时,有1≤y≤2014,符合闭函数的定义,故
反比例函数y=
| 2014 |
| x |
(2)分两种情况:k>0或k<0.
①当k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,故根据“闭函数”的定义知,
|
解得
|
∴此函数的解析式是y=x;
②当k<0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而减小,故根据“闭函数”的定义知,
|
解得
|
∴此函数的解析式是y=-x+m+n;
(3)∵y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴该二次函数的图象开口方向向上,最小值是-2,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.
①当c<2<d时,此时二次函数y=
| 1 |
| 2 |
d=
| 1 |
| 2 |
| 1 |
| 2 |
Ⅰ)当d=
| 1 |
| 2 |
| 1 |
| 2 |
Ⅱ)当d=
| 1 |
| 2 |
由于d>2,
所以d=6;
②当c≥2时,此二次函数y随x的增大而增大,则根据“闭函数”的定义知,
|
解得,
|
∵c<d,
∴
|
综上所述,c,d的值分别为-2,6.
点评:本题综合考查了二次函数图象的对称性和增减性,一次函数图象的性质以及反比例函数图象的性质.解题的关键是弄清楚“闭函数”的定义.解题时,也要注意“分类讨论”数学思想的应用.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.现在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为( )
如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.现在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为( )| A、15°或75° |
| B、20°或70° |
| C、20° |
| D、30° |
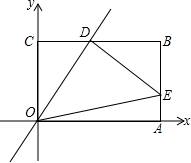 如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.
如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE. 已知:如图,在平面直角坐标系xOy中,点A(2
已知:如图,在平面直角坐标系xOy中,点A(2
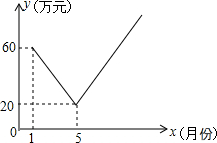 保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.
保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.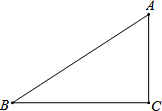 如图,在直角三角形ABC中,∠ACB=90°.
如图,在直角三角形ABC中,∠ACB=90°.