题目内容
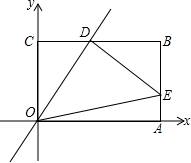 如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.
如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.(1)求证:△OCD∽△DBE;
(2)设CD=x,梯形OCBE的面积为S,求S与x之间的函数关系式;
(3)若梯形OCBE的面积是32,求D点坐标;
(4)当△ODE∽△OCD时,求正比例函数的解析式.
考点:相似形综合题
专题:
分析:(1)要证:△OCD∽△DBE,根据DE⊥OD,得到∠COD=∠BDE,根据四边形OACD是矩形,用“AA“可以判定相似;
(2)由△OCD∽△DBE,得到
=
,即:
=
,所以BE=
,再结合梯形的面积公式可以求得答案;
(3)由(2)的结论,令S=32,解相关一元二次方程即可得到答案.
(4)当△ODE∽△OCD时,又因为△OCD∽△DBE,所以△ODE∽△OCD∽△DBE,所以∠COD=∠DOE,∠BED=∠DEO,根据角平分线的性质可以确定D点的坐标,继而求得解析式.
(2)由△OCD∽△DBE,得到
| OC |
| BD |
| CD |
| BE |
| 6 |
| 8-x |
| x |
| BE |
| -x2+8x |
| 6 |
(3)由(2)的结论,令S=32,解相关一元二次方程即可得到答案.
(4)当△ODE∽△OCD时,又因为△OCD∽△DBE,所以△ODE∽△OCD∽△DBE,所以∠COD=∠DOE,∠BED=∠DEO,根据角平分线的性质可以确定D点的坐标,继而求得解析式.
解答:解:(1)∵DE⊥OD,所以∠CDO+∠BDE=90°,
又∵∠CDO+∠COD=90°,
∴∠COD=∠BDE,
又∵四边形OABC是矩形,
∴∠OCD=∠DBE=90°,
在△OCD和△DBE中
,
∴△OCD∽△DBE;
(2)∵CD=x,点B的坐标是(8,6),
∴BD=8-x,OC=6,
∵△OCD∽△DBE,
所以
=
,即:
=
,所以BE=
,
所以S=
=
×8=-
x2+
x+24
(3)由梯形OCBE的面积是32,所以-
x2+
x+24=32,解得:x1=2,x2=6,
∴D点的坐标为:(2,6),(6,6)
(4)当△ODE∽△OCD时,又∵△OCD∽△DBE,
∴△ODE∽△OCD∽△DBE,
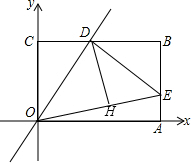
∴∠COD=∠DOE,∠BED=∠DEO,过点D做DH⊥OE,垂足为H,
根据角平分线的性质所以DC=DH=DB,所以点D为BC的中点,所以D点的坐标为(4,6),
∴所求的一次函数解析式为y=
x.
又∵∠CDO+∠COD=90°,
∴∠COD=∠BDE,
又∵四边形OABC是矩形,
∴∠OCD=∠DBE=90°,
在△OCD和△DBE中
|
∴△OCD∽△DBE;
(2)∵CD=x,点B的坐标是(8,6),
∴BD=8-x,OC=6,
∵△OCD∽△DBE,
所以
| OC |
| BD |
| CD |
| BE |
| 6 |
| 8-x |
| x |
| BE |
| -x2+8x |
| 6 |
所以S=
| (BE+OC)•BC |
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| 16 |
| 3 |
(3)由梯形OCBE的面积是32,所以-
| 2 |
| 3 |
| 16 |
| 3 |
∴D点的坐标为:(2,6),(6,6)
(4)当△ODE∽△OCD时,又∵△OCD∽△DBE,
∴△ODE∽△OCD∽△DBE,
∴∠COD=∠DOE,∠BED=∠DEO,过点D做DH⊥OE,垂足为H,
根据角平分线的性质所以DC=DH=DB,所以点D为BC的中点,所以D点的坐标为(4,6),
∴所求的一次函数解析式为y=
| 3 |
| 2 |

点评:掌握相似三角形的性质和判定,能够熟练运用勾股定理、待定系数法求得函数的解析式是解答本题的关键.在本题中要注意一元二次方程的解法,以及三角形相似对应边的确定.

练习册系列答案
相关题目
在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C为第一象限内一点,且AC=2,设tan∠BOC=m,则m的取值范围是( )
| A、m≥0 | ||||
B、m≥
| ||||
C、m≤
| ||||
D、0≤m≤
|

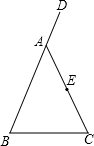 如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.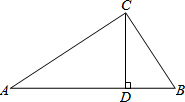 在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15,
在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15, 已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,联结AC、DF,∠A=∠D.
已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,联结AC、DF,∠A=∠D.