题目内容
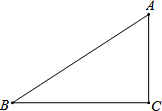 如图,在直角三角形ABC中,∠ACB=90°.
如图,在直角三角形ABC中,∠ACB=90°.(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,请你确定AB与所作⊙O的位置关系,直接写出你的结论.
考点:作图—复杂作图,直线与圆的位置关系
专题:
分析:(1)根据角平分线的作法作图即可;
(2)过O向AB作垂线,再根据角平分线的性质可得DO=CO,然后可得D在⊙O上,进而得到直线AB与⊙O相切.
(2)过O向AB作垂线,再根据角平分线的性质可得DO=CO,然后可得D在⊙O上,进而得到直线AB与⊙O相切.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)直线AB与⊙O相切;
理由:过O向AB作垂线,
∵BO平分∠ABC,
∴DO=CO,
∴D在⊙O上,
∴直线AB与⊙O相切.
 解:(1)如图所示:
解:(1)如图所示:(2)直线AB与⊙O相切;
理由:过O向AB作垂线,
∵BO平分∠ABC,
∴DO=CO,
∴D在⊙O上,
∴直线AB与⊙O相切.
点评:此题主要考查了复杂作图,以及直线与圆的位置关系,关键是掌握角平分线上的点到角两边的距离相等.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,联结AC、DF,∠A=∠D.
已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,联结AC、DF,∠A=∠D.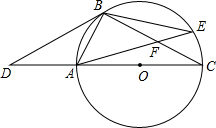 如图,D是⊙O直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,D是⊙O直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
 已知:如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,联结OD,作BE∥OD交⊙O于点E,联结DE并延长交BN于点C.
已知:如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,联结OD,作BE∥OD交⊙O于点E,联结DE并延长交BN于点C.
 如图,点A、B在反比例函数y=
如图,点A、B在反比例函数y=