题目内容
5.先化简,再求值:($\frac{{x}^{2}-1}{x-1}+x-3$)$÷\frac{x-1}{x+1}$,其中x=-$\frac{3}{2}$.分析 首先化简分式,进而利用分式乘除运算法则求出答案.
解答 解:($\frac{{x}^{2}-1}{x-1}+x-3$)$÷\frac{x-1}{x+1}$
=(x+1+x-3)•$\frac{x+1}{x-1}$
=(2x-2)•$\frac{x+1}{x-1}$
=2x+2,
当x=-$\frac{3}{2}$时,原式=2×(-$\frac{3}{2}$)+2=-1.
点评 此题主要考查了分式的混合运算,正确化简分式是解题关键.

练习册系列答案
相关题目
13.下列方程没有实数根的是( )
| A. | x2-3x+4=0 | B. | x2=2x | C. | 2x2+3x-1=0 | D. | x2+2x+1=0 |
20.下列计算正确的是( )
| A. | a6÷a3=a2 | B. | 3a2•2a=6a3 | C. | (3a)2=3a2 | D. | (a+b)2=a2+b2 |
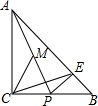 如图,△ACB为等腰直角三角形,△PBE也为等腰直角三角形,M为AP的中点.
如图,△ACB为等腰直角三角形,△PBE也为等腰直角三角形,M为AP的中点.
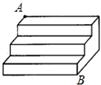 如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为125cm.
如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为125cm.