题目内容
1.图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3)…,则第6个图形的周长是( )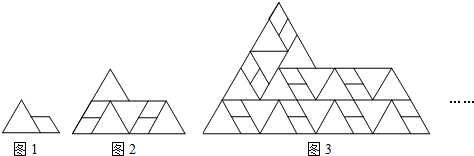
| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
分析 图1周长为1+$\frac{3}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}$=4=22,图2周长为2+3+1+1+1=2(1+$\frac{3}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}$)=8=23,图3周长为4+6+2+2+2=2(2+3+1+1+1)=16=24,…,由此得出一般规律.
解答 解:观察图形周长变化规律可知,图1周长为1+$\frac{3}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}$=4=22,图2周长为2+3+1+1+1=2(1+$\frac{3}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}$)=8=23,图3周长为4+6+2+2+2=2(2+3+1+1+1)=16=24,…,第6个图形的周长是26+1=128,
故选C.
点评 考查了规律型:图形的变化,本题是一道找规律的题目,关键是把各周长和的结果写成2的指数次方,得出指数与图形序号的关系.

练习册系列答案
相关题目
11.下列各数中,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{32}$ | C. | $\sqrt{96}$ | D. | $\sqrt{\frac{3}{4}}$ |
12.下列计算正确的是( )
| A. | x3+x3=x6 | B. | (m5)5=m10 | C. | x3÷x-1=x4 | D. | (-x5)(-x)3=-x2 |
13.下列方程没有实数根的是( )
| A. | x2-3x+4=0 | B. | x2=2x | C. | 2x2+3x-1=0 | D. | x2+2x+1=0 |
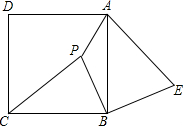 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.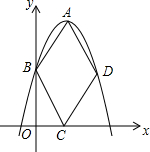 如图,在平面直角坐标系中,抛物线y=ax2-2ax+$\frac{3}{2}$(a<0)的顶点为A,与y轴的交点为B,点B关于抛物线对称轴的对称点为D,四边形ABCD为菱形,若点C在x轴上,则a的值为-$\frac{3}{2}$.
如图,在平面直角坐标系中,抛物线y=ax2-2ax+$\frac{3}{2}$(a<0)的顶点为A,与y轴的交点为B,点B关于抛物线对称轴的对称点为D,四边形ABCD为菱形,若点C在x轴上,则a的值为-$\frac{3}{2}$.