题目内容
5.阅读材料:写出二元一次方程x-3y=6的几个解:$\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,$\left\{\begin{array}{l}{x=6}\\{y=0}\end{array}\right.$,…,发现这些解的一般形式可表示为$\left\{\begin{array}{l}{x=3m}\\{y=m-2}\end{array}\right.$(m为有理数).把一般形式再变形为$\left\{\begin{array}{l}{m=\frac{x}{3}}\\{m=y+2}\end{array}\right.$,可得$\frac{x}{3}$=y+2,整理得原方程x-3y=6.根据阅读材料解答下列问题:若二元一次方程ax+by=c的解,可以写成$\left\{\begin{array}{l}{x=2n}\\{y=n+1}\end{array}\right.$(n为有理数),则a+b+c=-3或3.分析 根据题目中的信息可以求得a、b、c的值,从而可以求得a+b+c的值.
解答 解:∵$\left\{\begin{array}{l}{x=2n}\\{y=n+1}\end{array}\right.$(n为有理数),
∴$\left\{\begin{array}{l}{n=\frac{x}{2}}\\{n=y-1}\end{array}\right.$,
∴$\frac{x}{2}=y-1$,
∴x-2y=-2或-x+2y=2,
∵二元一次方程ax+by=c的解,可以写成$\left\{\begin{array}{l}{x=2n}\\{y=n+1}\end{array}\right.$(n为有理数),
∴a=1,b=-2,c=-2或a=-1,b=2,c=2,
∴a+b+c=1+(-2)+(-2)=-3或a+b+c=(-1)+2+2=3,
故答案为:-3或3.
点评 本题考查二元一次方程的解,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
20.若A=3m2-5m+2,B=3m2-5m-2,则A与B的大小关系是( )
| A. | A=B | B. | A>B | C. | A<B | D. | 无法确定 |
 △ABC中,∠A=30°,∠B=45°,AC=4,求AB的长?
△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长?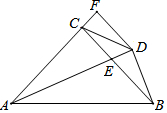 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论: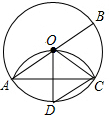 已知:如图,AB是⊙O的直径,AC是弦,将劣弧$\widehat{AC}$沿弦AC翻折与AB的交点恰好是圆心O,连接BC,作半径OD⊥AC.求证:四边形BCDO是菱形.
已知:如图,AB是⊙O的直径,AC是弦,将劣弧$\widehat{AC}$沿弦AC翻折与AB的交点恰好是圆心O,连接BC,作半径OD⊥AC.求证:四边形BCDO是菱形.