题目内容
10.计算:$\frac{\frac{1}{2}}{1+\frac{1}{2}}$+$\frac{\frac{1}{3}}{(1+\frac{1}{2})(1+\frac{1}{3})}$+$\frac{\frac{1}{4}}{(1+\frac{1}{2})(1+\frac{1}{3})(1+\frac{1}{4})}$+…+$\frac{\frac{1}{2016}}{(1+\frac{1}{2})(1+\frac{1}{3})…(1+\frac{1}{2016})}$.分析 先计算每一个分数,再找出规律:$\frac{1}{2}$×$\frac{2}{3}$+$\frac{1}{3}$×$\frac{2}{4}$+$\frac{1}{4}$×$\frac{2}{5}$+…+$\frac{1}{2016}$×$\frac{2}{2017}$,再转化成2($\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{2016×2017}$)=2($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$),计算即可.
解答 解:原式=$\frac{1}{2}$×$\frac{2}{3}$+$\frac{1}{3}$×$\frac{2}{4}$+$\frac{1}{4}$×$\frac{2}{5}$+…+$\frac{1}{2016}$×$\frac{2}{2017}$,
=2×($\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{2016×2017}$)
=2×($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$)
=2×($\frac{1}{2}$-$\frac{1}{2017}$)
=2×$\frac{2017-2}{2×2017}$
=$\frac{2015}{2017}$.
点评 本题考查了分式的加减,把原分式化简,找到规律$\frac{1}{2}$×$\frac{2}{3}$+$\frac{1}{3}$×$\frac{2}{4}$+$\frac{1}{4}$×$\frac{2}{5}$+…+$\frac{1}{2016}$×$\frac{2}{2017}$=2×($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$)是解题的关键.

 如图①,天平呈平衡状态,其中左侧盘中有一袋玻璃球,右侧盘中也有一袋玻璃球,还有2个各20g的砝码.现将左侧袋中一颗玻璃球移至右侧盘,并拿走右侧盘中的1个砝码,天平仍呈平衡状态,如图②.则移动的玻璃球质量为( )
如图①,天平呈平衡状态,其中左侧盘中有一袋玻璃球,右侧盘中也有一袋玻璃球,还有2个各20g的砝码.现将左侧袋中一颗玻璃球移至右侧盘,并拿走右侧盘中的1个砝码,天平仍呈平衡状态,如图②.则移动的玻璃球质量为( )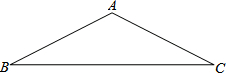 在△ABC中,AB=AC
在△ABC中,AB=AC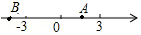 点A,B在数轴上的位置如图所示,其对应的数分别是a和b.对于以下结论:
点A,B在数轴上的位置如图所示,其对应的数分别是a和b.对于以下结论: