题目内容
15.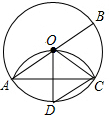 已知:如图,AB是⊙O的直径,AC是弦,将劣弧$\widehat{AC}$沿弦AC翻折与AB的交点恰好是圆心O,连接BC,作半径OD⊥AC.求证:四边形BCDO是菱形.
已知:如图,AB是⊙O的直径,AC是弦,将劣弧$\widehat{AC}$沿弦AC翻折与AB的交点恰好是圆心O,连接BC,作半径OD⊥AC.求证:四边形BCDO是菱形.
分析 先证明四边形OADC是菱形,得OA∥DC,AO=DC,根据同圆的半径相等得:AO=OB,所以OB=DC,OB∥DC,且OB=OD,所以四边形BCDO是菱形.
解答 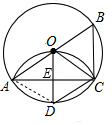 证明:连接AD,
证明:连接AD,
∵OD⊥AC,
∴AE=EC,
由翻折得:AC是OD的垂直平分线,
∴OE=DE,
∵OA=OC,
∴四边形OADC是菱形,
∴OA∥DC,AO=DC,
∵AO=OB,
∴OB=DC,OB∥DC,
∴四边形BCDO是平行四边形,
∵OB=OD,
∴四边形BCDO是菱形.
点评 本题是圆与四边形的综合题,难度不大,考查了平行四边形、菱形、垂径定理和翻折变换的性质,明确翻折前后重合的点是对称点,对称点的连线被折痕垂直平分,熟练掌握菱形的判定:①四边相等的四边形是菱形,②有一组邻边相等的平行四边形是菱形,③对角线互相垂直的平行四边形是菱形.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图所示,AD∥BC,AB∥DC,M,Q分别在DA、BC的最长线上,且AM=CQ,连接MQ,分别交CD,BD,AB于点P,E,N,求证:△AMN≌△CQP.
如图所示,AD∥BC,AB∥DC,M,Q分别在DA、BC的最长线上,且AM=CQ,连接MQ,分别交CD,BD,AB于点P,E,N,求证:△AMN≌△CQP.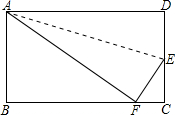 长方形纸片ABCD,沿AE折叠边AD,使点D落在BC边上的点F处,AB=5,S△ABF=30,求EC.
长方形纸片ABCD,沿AE折叠边AD,使点D落在BC边上的点F处,AB=5,S△ABF=30,求EC.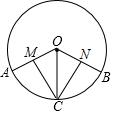 如图,OA、OB、OC是⊙O的半径,$\widehat{AC}$=$\widehat{BC}$,CM⊥OA于M,CN⊥OB于N,求证:MC=NC.
如图,OA、OB、OC是⊙O的半径,$\widehat{AC}$=$\widehat{BC}$,CM⊥OA于M,CN⊥OB于N,求证:MC=NC.