题目内容
12. 如下图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,则这个矩形对角线的长是( )
如下图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,则这个矩形对角线的长是( )| A. | 2.5 | B. | 5 | C. | 6 | D. | 7.5 |
分析 根据矩形的对角线互相平分且相等可得OA=OB=$\frac{1}{2}$AC,根据邻补角的定义求出∠AOB,然后判断出△AOB是等边三角形,根据等边三角形的性质可得OA=AB,然后求解即可.
解答 解:在矩形ABCD中,OA=OB=$\frac{1}{2}$AC,
∵∠AOD=120°,
∴∠AOB=180°-∠AOD=180°-120°=60°,
∴△AOB是等边三角形,
∴OA=AB=2.5,
∴AC=2OA=2×2.5=5.
故选B.
点评 本题考查了矩形的性质,等边三角形的判定与性质,熟记矩形的对角线互相平分且相等,证明三角形是等边三角形是解题的关键.

练习册系列答案
相关题目
3.一项工程甲队单独完成需要x天,乙队单独完成所用的时间比甲队单独完成所用的时间多5天,现在先由乙队做x天,剩下由甲、乙两队合作2天完成,求x的值,根据题意列方程正确的是( )
| A. | $\frac{2}{x}$+$\frac{x+2}{x+5}$=1 | B. | $\frac{2}{x}$+$\frac{x}{x+5}$=1 | C. | $\frac{2}{x}$+$\frac{x}{x-5}$=1 | D. | $\frac{2}{x}$+$\frac{x+2}{x-5}$=1 |
20.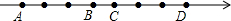 已知如图:数轴上A,B,C,D四点对应的有理数分别是整数a,b,c,d.且有c-2a=7,则原点应是( )
已知如图:数轴上A,B,C,D四点对应的有理数分别是整数a,b,c,d.且有c-2a=7,则原点应是( )
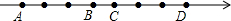 已知如图:数轴上A,B,C,D四点对应的有理数分别是整数a,b,c,d.且有c-2a=7,则原点应是( )
已知如图:数轴上A,B,C,D四点对应的有理数分别是整数a,b,c,d.且有c-2a=7,则原点应是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
2. 如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
 如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )| A. | 100° | B. | 110° | C. | 115° | D. | 120° |
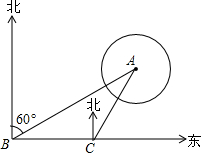 如图,某公园有一小亭A,它周围100米内是文物保持区,某勘探队员在公园由西向东行走,在B处测得小亭A在北偏东60°的方向上,行走200米后到达C处,此时测得小亭A在北偏东30°的方向上,若该公园打算沿BC的方向修一条笔直的小路,则此小路是否会通过文物保护区?请通过计算说明.
如图,某公园有一小亭A,它周围100米内是文物保持区,某勘探队员在公园由西向东行走,在B处测得小亭A在北偏东60°的方向上,行走200米后到达C处,此时测得小亭A在北偏东30°的方向上,若该公园打算沿BC的方向修一条笔直的小路,则此小路是否会通过文物保护区?请通过计算说明.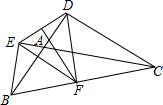 如图,已知钝角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点,连结DM、ME,若∠BAC=116°,则∠DME=52度.
如图,已知钝角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点,连结DM、ME,若∠BAC=116°,则∠DME=52度.