题目内容
18.解方程:(3x-5)(5-3x)+(3x-1)2=10.分析 先将(3x-5)(5-3x)变形为-(3x-5)2,然后利用平方差公式分解因式,从而可将原方程化简为一元一次方程,最后解这个一元一次方程即可.
解答 解:(3x-5)(5-3x)+(3x-1)2=10,
∴(3x-1)2-(3x-5)2=10.
∴(3x-1-3x+5)(3x-1+3x-5)=10.
∴4(6x-6)=10.
24x-24=10.
∴24x=34.
解得:x=$\frac{17}{12}$.
点评 本题主要考查的是平方差公式、完全平方公式的应用、解一元一次方程,掌握平方差公式和完全平方公式是解题的关键.

练习册系列答案
相关题目
8.下列式子中表示y是x的反比例函数的是( )
| A. | y=2x-3 | B. | xy=5 | C. | y=$\frac{2}{x^2}$ | D. | y=$\frac{1}{4}$x |
3.如果-ax2yb(a,b为常数)是四次单项式,那么b的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
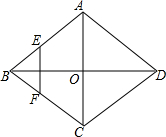 如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为4$\sqrt{7}$.
如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为4$\sqrt{7}$. 如图,在△ABC中,AB=AC,∠A=35°,以B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则∠ABD的度数为37.5°.
如图,在△ABC中,AB=AC,∠A=35°,以B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则∠ABD的度数为37.5°.
 如图,在等腰梯形ABCD中.AD∥BC,过C作CE∥AB.P为梯形ABCD内一点,连结BP并延长交CD于F,交CE于E,再连结PC.若BP=PC.求证:△PFC∽△PCE.
如图,在等腰梯形ABCD中.AD∥BC,过C作CE∥AB.P为梯形ABCD内一点,连结BP并延长交CD于F,交CE于E,再连结PC.若BP=PC.求证:△PFC∽△PCE.