题目内容
9.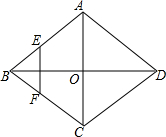 如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为4$\sqrt{7}$.
如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为4$\sqrt{7}$.
分析 由菱形的性质得出AB=BC=CD=AD,AC⊥BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD=2,证出EF是△ABC的中位线,由三角形中位线定理得出AC=2EF=2$\sqrt{3}$,得出OA=$\sqrt{3}$,由勾股定理求出AB,即可求出菱形的周长.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD=2,
∴∠AOB=90°,
∵E、F分别是AB、BC边上的中点,
∴EF是△ABC的中位线,
∴AC=2EF=2$\sqrt{3}$,
∴OA=$\sqrt{3}$,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{2}^{2}}$=$\sqrt{7}$,
∴菱形ABCD的周长=4AB=4$\sqrt{7}$;
故答案为:4$\sqrt{7}$.
点评 本题考查了菱形的性质、三角形中位线定理、勾股定理;熟练掌握菱形的性质,由三角形中位线定理得出AC,由勾股定理求出AB是解决问题的关键.

练习册系列答案
相关题目
 如图,AB、CD是⊙O的直径,AB∥DE,AC=3,则AE=3.
如图,AB、CD是⊙O的直径,AB∥DE,AC=3,则AE=3.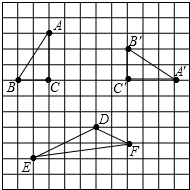 如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,解决下面的问题:
如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,解决下面的问题: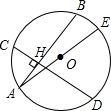 如图,在⊙O中,弦AB⊥CD,H为垂足,AE是O的直径.求证:HA2+HD2+HC2+HB2=AE2.
如图,在⊙O中,弦AB⊥CD,H为垂足,AE是O的直径.求证:HA2+HD2+HC2+HB2=AE2.