题目内容
13.在平面直角坐标系中,点O为坐标原点,A,B分别为y轴、x轴上的点,链接AB,B点坐标为(8,0),∠OAB=45°,C是AB中点.
(1)如图1,求C点坐标;
(2)如图2,P为线段AC上一点(不与A、C重合),连接OP,过B作OP的垂线,垂足为Q,连接CQ,求∠CQP的度数;
(3)在(2)的条件下,如图3,过O作OE⊥OP,在OE上取一点M,连接MB,使∠MBO=∠CQP,连接PM,交x轴于点N,连接OF,若F为BP垂直平分线上的点,当∠FNO=3∠FON时,求点P的坐标.
分析 (1)如图1,过C作CE⊥OB于E,过C作CF⊥OA于F,根据三角形的中位线的性质就看得到结论;
(2)如图2,连接OC,根据等腰直角三角形的性质得到OC⊥AB,由BQ⊥OP,得到∠PQB=∠PCO,推出△POC∽△PQB,根据相似三角形的性质得到$\frac{PC}{PO}=\frac{PQ}{PB}$,证得△PQC∽△PBO,即可得到结论;
(3)如图3,连接BF,过P作PH⊥OB于H,由∠MBO=∠CQP=45°,得到∠PBM=90°,根据线段垂直平分线的性质得到PF=FB,由等腰三角形的性质得到∠FPB=∠PBF,根据余角的性质得到∠FBM=∠FMB,等量代换得到OF=BF,证得∠FOB=∠FBO,设∠FOB=∠FBO=α,则∠FNO=3α,根据外角的性质得到∠MFB=2α,由三角形的内角和得到α=22.5°,求出∠FNO=67.5°,∠FON=22.5°,推出△POM是等腰直角三角形,得到OP=OM,∠OPM=45°,通过△POH∽△PBM,得到∠PON=∠BMN=67.5°,根据相似三角形的性质得到$\frac{OH}{BM}=\frac{OP}{PM}=\frac{\sqrt{2}}{2}$,求得BN=BM=$\sqrt{2}$OH,由OB=8,列方程解得OH=8-4$\sqrt{2}$,于是得到结论.
解答  解:(1)如图1,过C作CE⊥OB于E,过C作CF⊥OA于F,
解:(1)如图1,过C作CE⊥OB于E,过C作CF⊥OA于F,
∴CE∥OA,CF∥OB,
∵C是AB中点,
∴CE=$\frac{1}{2}$OA,CF=$\frac{1}{2}$OB,
∵∠AOB=90°,∠OAB=45°,
∴OA=OB,
∵B点坐标为(8,0),
∴OB=8,
∴C(4,4);
(2)如 图2,连接OC,
图2,连接OC,
∵△AOB是等腰直角三角形,C是AB中点,
∴OC⊥AB,
∵BQ⊥OP,
∴∠PQB=∠PCO,
∵∠QPC=∠CPQ,
∴△POC∽△PQB,
∴$\frac{PC}{PO}=\frac{PQ}{PB}$,
∴△PQC∽△PBO,
∴∠PQC=∠ABO=45°;
(3)如图3,连接BF,过P作PH⊥OB于H, ∵∠MBO=∠CQP=45°,
∵∠MBO=∠CQP=45°,
∴∠PBM=90°,
∵F为BP垂直平分线上的点,
∴PF=FB,
∴∠FPB=∠PBF,
∵∠BPF+∠BMP=∠PBF+∠FBM=90°,
∴∠FBM=∠FMB,
∴FB=FM,
∴PF=FM,
∵∠POM=90°,
∴PF=FM=OF,
∴OF=BF,
∴∠FOB=∠FBO,
∵∠FNO=3∠FON,
∴∠FNO=3∠FBO,
设∠FOB=∠FBO=α,则∠FNO=3α,
∴∠MFB=2α,
∴∠FMB=∠FBM=45°+α,
∴2α+2(45°+α)=180°,
解得:α=22.5°,
∴∠FNO=67.5°,∠FON=22.5°,
∴∠OFN=90°,
∴OF⊥PM,
∴△POM是等腰直角三角形,
∴OP=OM,∠OPM=45°,
∵∠HPB=∠PBH=45°,
∴∠OPH=∠BPM,
∵∠PHO=∠PBM=90°,
∴△POH∽△PBM,
∴∠PON=∠BMN=67.5°,
∵∠PNO=∠BNO,
∴∠OPN=∠NBM=45°,
∴∠PNO=67.5°,
∴∠PON=∠PNO,
∴OP=PN,
∴BN=BM,OH=HN,
∵△POH∽△PBM,
∴$\frac{OH}{BM}=\frac{OP}{PM}=\frac{\sqrt{2}}{2}$,
∴BN=BM=$\sqrt{2}$OH,
∵OB=8,
∴OH+HN+BN=OH+OH+$\sqrt{2}$OH=8,
解得OH=8-4$\sqrt{2}$,
∴BH=PH=4$\sqrt{2}$,
∴P(8-4$\sqrt{2}$,4$\sqrt{2}$).
点评 本题考查了等腰直角三角形的性质和判定,等腰三角形的性质,线段垂直平分线的性质,相似三角形的判定和性质,外角的性质,三角形的内角和,三角形中位线的性质,正确的周长辅助线是解题的关键.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案| A. | 12 | B. | 12或66 | C. | 15 | D. | 33 |
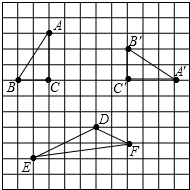 如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,解决下面的问题:
如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,解决下面的问题: 如图,在完全重合放置的两张长方形纸片ABCD中,AB=4,BC=8,将上面的纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为点G,连接DG,求图中阴影部分的面积.
如图,在完全重合放置的两张长方形纸片ABCD中,AB=4,BC=8,将上面的纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为点G,连接DG,求图中阴影部分的面积. 如图所示,化简|a|-|c|+|a-c|-2|c-b|+|b+c|.
如图所示,化简|a|-|c|+|a-c|-2|c-b|+|b+c|.