题目内容
7.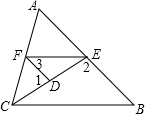 如图,已知∠1+∠2=180°,∠B=∠3.
如图,已知∠1+∠2=180°,∠B=∠3.(1)求证:∠AFE=∠ACB;
(2)若CE平分∠ACB,且∠1=82°,∠3=50°,求∠AFE的度数.
分析 (1)求出∠FDE=∠2,根据三角形内角和定理求出∠FEC=∠ECB,根据平行线的判定得出EF∥BC,根据平行线的性质得出即可;
(2)根据三角形外角性质求出∠FEC=∠1-∠3=32°,求出∠FEC=∠ECB=32°,根据角平分线定义得出∠ACB=2∠ECB=64°,即可得出答案.
解答 (1)证明:∵∠1+∠2=180°,∠1+∠FDE=180°,
∴∠FDE=∠2,
∵∠3+∠FEC+∠FDE=180°,∠2+∠B+∠ECB=180°,∠B=∠3,
∴∠FEC=∠ECB,
∴EF∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=82°,∠3=50°,
∴∠FEC=∠1-∠3=32°,
∵∠FEC=∠ECB,
∴∠ECB=32°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=64°,
∴∠AFE=∠ACB=64°.
点评 本题考查了平行线的性质和判定,三角形内角和定理,三角形外角性质的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
17. 如图,在等腰梯形ABCD中AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是( )
如图,在等腰梯形ABCD中AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是( )
 如图,在等腰梯形ABCD中AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是( )
如图,在等腰梯形ABCD中AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是( )| A. | 14cm | B. | 15cm | C. | 16cm | D. | 17cm |
16.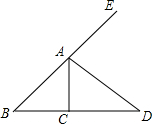 如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
 如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )| A. | 25° | B. | 85° | C. | 60° | D. | 95° |
 如图,与∠CAB成内错角的是∠HCA,∠ABI.
如图,与∠CAB成内错角的是∠HCA,∠ABI.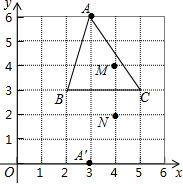 如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).
如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).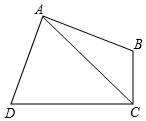 如图,四边形ABCD中,∠A=∠C=90度,AB=AD,若这个四边形的面积为24,则AC的长是4$\sqrt{3}$.
如图,四边形ABCD中,∠A=∠C=90度,AB=AD,若这个四边形的面积为24,则AC的长是4$\sqrt{3}$.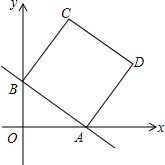 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.