题目内容
8.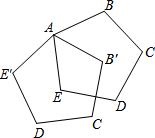 如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.
如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.
分析 DE与B′C′相交于O点,如图,利用正五边形的性质计算出∠B=∠BAE=∠E=108°,再根据旋转的性质得∠BAB′=α,∠B′=∠B=108°,接着根据四边形内角和计算出∠B′AE的度数,然后计算∠BAE-∠B′AE即可.
解答 解:DE与B′C′相交于O点,如图,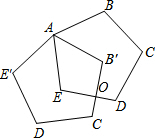
∵五边形ABCDE为正五边形,
∴∠B=∠BAE=∠E=$\frac{(5-2)×180°}{5}$=108°,
∵正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),
∴∠BAB′=α,∠B′=∠B=108°,
∵DE⊥B′C′,
∴∠B′OE=90°,
∴∠B′AE=360°-∠B′-∠E-∠B′OE=360°-108°-108°-90°=54°,
∴∠BAB′=∠BAE-∠B′AE=108°-54°=54°,
即∠α=54°.
故答案为54.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是计算正五边形的内角.

练习册系列答案
相关题目
17.武汉市在一次扶贫助残活动中,捐款约5180000元,请将5180000元用科学记数法表示为( )
| A. | 0.518×107元 | B. | 5.18×106元 | C. | 51.8×105元 | D. | 518×104元 |
 如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍.
如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍.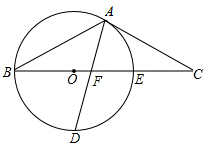 如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且AC是切线,⊙O与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F.
如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且AC是切线,⊙O与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F.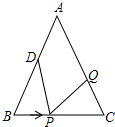 如图,已知△ABC中AB=AC=12厘米,BC=9厘米,点D为AB的中点.
如图,已知△ABC中AB=AC=12厘米,BC=9厘米,点D为AB的中点. 如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.
如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.