题目内容
4. 如图,D,E,F分别是△ABC边上一点,且AD=AF,BD=BE.
如图,D,E,F分别是△ABC边上一点,且AD=AF,BD=BE.(1)若∠C=80°,求∠EDF的度数;
(2)若∠C=α,直接写出∠EDF的度数$\frac{1}{2}$(180-α)°.
分析 (1)根据等腰三角形的性质可求得∠1=∠2∠3=∠4,再结合三角形内角和定理,可用∠B和∠C分别表示出∠2和∠4,结合平角的定义,可找到∠2+∠EDF+∠4=180°,可求得∠EDF的大小;
(2)方法同(1).
解答  解:(1)∵∠A+∠B+∠C=180°,∠C=80°,
解:(1)∵∠A+∠B+∠C=180°,∠C=80°,
∴∠A+∠B=100°,
∵AD=AF,BD=BE,
∴∠1=∠2,∠3=∠4,
∵∠A+∠1+∠2=180°,∠B+∠3+∠4=180°,
∴∠2=$\frac{1}{2}$(180°-∠A),∠4=$\frac{1}{2}$(180°-∠B),
∵∠2+∠EDF+∠4=180°,
∴∠EDF=180°-∠2-∠4
=180°-$\frac{1}{2}$(180°-∠A)-$\frac{1}{2}$(180°-∠B)
=50°;
(2)∵∠A+∠B+∠C=180°,∠C=α,
∴∠A+∠B=180°-α,
∵AD=AF,BD=BE,
∴∠1=∠2,∠3=∠4,
∵∠A+∠1+∠2=180°,∠B+∠3+∠4=180°,
∴∠2=$\frac{1}{2}$(180°-∠A),∠4=$\frac{1}{2}$(180°-∠B),
∵∠2+∠EDF+∠4=180°,
∴∠EDF=180°-∠2-∠4
=180°-$\frac{1}{2}$(180°-∠A)-$\frac{1}{2}$(180°-∠B)
=$\frac{1}{2}$(180-α)°,
故答案为:$\frac{1}{2}$(180-α)°.
点评 本题主要考查等腰三角形的性质和三角形内角和定理,根据等边对等角和三角形内角和定理,找到∠A、∠B和∠EDF的关系是解题的关键.

练习册系列答案
相关题目

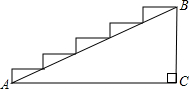 如图所示,在高为2m,坡度为30°的楼梯上铺地毯,已知地毯的单价为100元/米2,地毯宽为2m,求购此地毯的费用为多少?(结果保留整数)
如图所示,在高为2m,坡度为30°的楼梯上铺地毯,已知地毯的单价为100元/米2,地毯宽为2m,求购此地毯的费用为多少?(结果保留整数)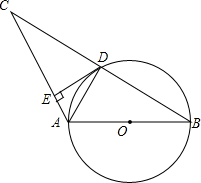 如图,AB是⊙0的直径,⊙0经过△ABC的边BC的中点D,DE⊥AC,垂足为E.
如图,AB是⊙0的直径,⊙0经过△ABC的边BC的中点D,DE⊥AC,垂足为E.