题目内容
14.下列等式从左边到右边是怎样得到的?(1)$\frac{{x}^{2}-6x+9}{x-3}$=x-3;
(2)x-y=$\frac{{x}^{2}-{y}^{2}}{y+x}$(x+y≠0)
分析 (1)根据分式的基本性质,把左边分式的分子、分母同时除以x-3,即可得到x-3.
(2)首先把x-y看成$\frac{x-y}{1}$,然后根据分式的基本性质,把分子、分母同时乘以x+y,即可得到$\frac{{x}^{2}{-y}^{2}}{y+x}$.
解答 解:(1)$\frac{{x}^{2}-6x+9}{x-3}$=$\frac{{(x-3)}^{2}}{x-3}$=$\frac{{(x-3)}^{2}÷(x-3)}{(x-3)÷(x-3)}$=x-3
(2)∵x+y≠0,
∴x-y=$\frac{(x-y)(x+y)}{x+y}$=$\frac{{x}^{2}-{y}^{2}}{y+x}$.
点评 此题主要考查了分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变,要熟练掌握.

练习册系列答案
相关题目
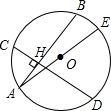 如图,在⊙O中,弦AB⊥CD,H为垂足,AE是O的直径.求证:HA2+HD2+HC2+HB2=AE2.
如图,在⊙O中,弦AB⊥CD,H为垂足,AE是O的直径.求证:HA2+HD2+HC2+HB2=AE2. 如图,A、B在x轴上,直线PA:y=x+1与直线PB:y=-2x+m(m>1)交于P.
如图,A、B在x轴上,直线PA:y=x+1与直线PB:y=-2x+m(m>1)交于P. 如图所示,化简|a|-|c|+|a-c|-2|c-b|+|b+c|.
如图所示,化简|a|-|c|+|a-c|-2|c-b|+|b+c|. 如图,D,E,F分别是△ABC边上一点,且AD=AF,BD=BE.
如图,D,E,F分别是△ABC边上一点,且AD=AF,BD=BE.