题目内容
18.一个游戏如下:交1元钱可分别转动甲乙两个转盘各一次(甲盘平均分成4份,白色1份),(乙盘平均分成3份,白色1份),甲乙两盘其余均为黑色,若转盘停止时两指针的指向为表中的组合,则可获得相应奖金:| 两转盘颜色(甲,乙) | (黑,黑) | (黑,白) | (白,黑) | (白,白) |
| 中奖金额 | 0元 | 1元 | 2元 | 3元 |
(2)如果参与多次游戏,那么游戏者平均每次获奖的预期是多少元?这个游戏对游戏参加者是否有利?
分析 (1)画出树状图,然后根据概率公式解答即可;
(2)根据加权平均数的计算方法列式计算即可得解.
解答 解:(1)甲图黑、白的比为3:1,不妨设四部分分别为黑1、黑2、黑3、白,
乙图的黑白的比为2:1,不妨设三部分分别为黑1、黑2、白,
画出树状图如下:
一共有12种情况,获得3元的(白,白)只有1种情况,
所以,获得3元的概率=$\frac{1}{12}$;
(2)平均每次的收益=$\frac{12-6×0-3×1-2×2-1×3}{12}$=$\frac{1}{6}$元.
点评 本题考查了列表法和树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.张华的身份证号码是320826198309216851,请问张华是( )月出生的?
| A. | 3月 | B. | 6月 | C. | 9月 | D. | 12月 |
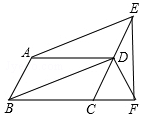 如图,平行四边形ABCD中,点E、F分别在CD、BC的延长线上,AE∥BD.
如图,平行四边形ABCD中,点E、F分别在CD、BC的延长线上,AE∥BD.
 如图,已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点($\frac{1}{2}$,8),直线y=-x+b经过该反比例函数图象上的点Q(4,m).
如图,已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点($\frac{1}{2}$,8),直线y=-x+b经过该反比例函数图象上的点Q(4,m).