题目内容
8.化简求值:(1)(a+b)(a-b)+(a+b)2,其中a=3,b=-$\frac{1}{3}$.
(2)已知2x-y=10,求[(x2+y2)-(x-y)2+2y(x-y)]÷4y的值.
分析 根据整式的运算法则即可求出答案.
解答 解:(1)当a=3,b=-$\frac{1}{3}$时,
∴原式=a2-b2+a2+2ab+b2
=2a2+2ab
=2×9+2×3×(-$\frac{1}{3}$)
=18-2
=17
(2)当2x-y=10时,
原式=[x2+y2-(x2-2xy+y2)+2xy-2y2]÷4y
=x-$\frac{1}{2}$y
=$\frac{1}{2}$(2x-y)
=5
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列判断正确的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 在同一平面内,a⊥b,b⊥c,则c⊥a | |
| C. | 同旁内角互补,则它们的角平分线互相垂直 | |
| D. | 经过一点有且只有一条直线与已知直线平行 |
18.一个游戏如下:交1元钱可分别转动甲乙两个转盘各一次(甲盘平均分成4份,白色1份),(乙盘平均分成3份,白色1份),甲乙两盘其余均为黑色,若转盘停止时两指针的指向为表中的组合,则可获得相应奖金:
(1)通过树状图或表格求获得3元奖的概率.
(2)如果参与多次游戏,那么游戏者平均每次获奖的预期是多少元?这个游戏对游戏参加者是否有利?
| 两转盘颜色(甲,乙) | (黑,黑) | (黑,白) | (白,黑) | (白,白) |
| 中奖金额 | 0元 | 1元 | 2元 | 3元 |
(2)如果参与多次游戏,那么游戏者平均每次获奖的预期是多少元?这个游戏对游戏参加者是否有利?
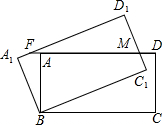 如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为=2-$\sqrt{3}$.
如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为=2-$\sqrt{3}$. 如图,已知∠1+∠2=180°,∠3=108°.求∠4的度数.
如图,已知∠1+∠2=180°,∠3=108°.求∠4的度数.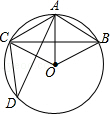 如图,在半径为6 cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BDC}$上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3$\sqrt{3}{cm}$;③∠AOB=60°;④四边形ABOC是菱形,其中正确结论的序号是①③④.
如图,在半径为6 cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BDC}$上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3$\sqrt{3}{cm}$;③∠AOB=60°;④四边形ABOC是菱形,其中正确结论的序号是①③④.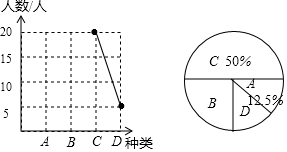 巴蜀中学2017春季运动会的开幕式精彩纷呈,主要分为以下几个类型:A文艺范、B动漫潮、C学院派、D民族风,为了解未能参加运动会的初三学子对开幕式类型的喜好情况,学生处在初三年级随机抽取了一部分学生进行调查,并将他们喜欢的种类绘制成如下统计图,请你根据统计图解答以下问题:
巴蜀中学2017春季运动会的开幕式精彩纷呈,主要分为以下几个类型:A文艺范、B动漫潮、C学院派、D民族风,为了解未能参加运动会的初三学子对开幕式类型的喜好情况,学生处在初三年级随机抽取了一部分学生进行调查,并将他们喜欢的种类绘制成如下统计图,请你根据统计图解答以下问题: