Question

6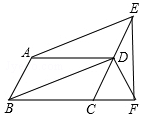．如图，平行四边形ABCD中，点E、F分别在CD、BC的延长线上，AE∥BD．
（1）求证：D是EC中点；
（2）若∠ABC=60°，EF⊥BF于点F，CF=2，求AB的长，并直接写出图中与CF相等的线段．

Answer 1

分析 （1）根据平行四边形性质推出AB=CD，AB∥CD，得出平行四边形ABDE，推出DE=DC=AB，进而可证明点D为CE的中点；
（2）根据直角三角形性质求出CE长，利用平行四边形的性质求出AB的长即可；利用直角三角形30度角的性质即可判断与CF相等的线段；

解答 解：（1）∵四边形ABCD是平行四边形，
∴AB∥DC，AB=CD，
∵AE∥BD，
∴四边形ABDE是平行四边形．
∴AB=DE=CD，即D为CE中点．

（2）∵EF⊥BC，
∴∠EFC=90°．
∵AB∥CD，
∴∠DCF=∠ABC=60°．
∴∠CEF=30°．
∵CF=2，
∴CE=2CF=4，
∴CD=DE=2，
∴AB=CD=2，
图中与CF相等的线段有：CD、DE、AB、DF．

点评 本题考查了平行四边形的性质和判定，平行线性质，勾股定理，直角三角形斜边上中线性质，含30度角的直角三角形性质等知识点的应用，此题综合性比较强，是一道比较好的题目．