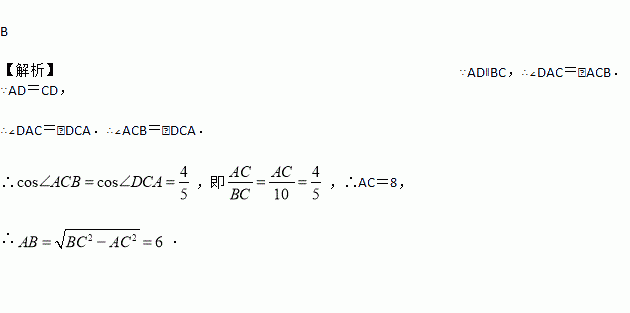题目内容
如图，在四边形ABCD中，AD∥BC，AC⊥AB，AD=CD，cos ∠DCA=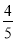
，BC=10，则AB的值是( )
A. 3 B. 6 C. 8 D. 9
B
【解析】∵AD∥BC，∴∠DAC＝∠ACB．∵AD＝CD，
∴∠DAC＝∠DCA．∴∠ACB＝∠DCA．
∴，即，∴AC＝8，
∴．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如图，直线AB∥ CD，∠ B=50°，∠ C=40°，则∠E等于（ ）
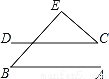
A. 70° B. 80° C. 90° D. 100°
C
【解析】试题分析：根据平行线的性质得到∠1=∠B=50°，由三角形的内角和定理可得∠E=180°﹣∠B﹣∠1=90°，故答案选C． 解方程：
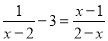
x＝3
【解析】试题分析：按照解分式方程的步骤解方程即可.
试题解析：去分母，得
去括号，得
移项，得
合并同类项，得
系数化为1，得
检验：当时，
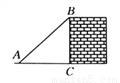
是原方程的解. 如图所示，一架梯子斜靠在墙上，若梯子底端到墙的距离AC=3米，cos∠BAC＝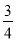
，则梯子AB的长度为______米．
4
【解析】在Rt△BCA中，AC＝3米，cos∠BAC＝，所以AB＝4米，即梯子的长度为4米． 等腰三角形一腰上的高与腰长之比是1?2，则等腰三角形顶角的度数为( )
A. 30° B. 50° C. 60°或120° D. 30°或150°
D
【解析】如图1，当高BD在三角形的内部时，
∵高BD是腰长AB的一半，
∴sin A＝，∴∠A＝30°；
如图2，当高CD在三角形的外部时，
∵高CD是腰长AC的一半，
∴sin∠1＝，∴∠1＝30°，
∴∠BAC=180°-30°=150°，
∴该三角形的顶角的度数是30°或150°，
故选D． 计算：17×3.14＋61×3.14＋22×3.14；
314
【解析】试题分析：根据提公因式法分解因式，先确定公因式3.14，再提取公因式即可.
试题解析：17×3.14＋61×3.14＋22×3.14
=3.14×（17+61+22）
=3.14×100
=314 4x(m－n)＋8y(n－m)2中各项的公因式是________.
4(m－n)
【解析】根据题意，先变形为4x(m－n)＋8y(m－n)2，把m-n看做一个整体，即可找到公因式4（m-n）.
故答案为：4（m-n）. 如图所示，△DEF是由△ABC经过平移得到的，若∠B=50°,∠C=75°,则∠D=_____，∠E＝________.
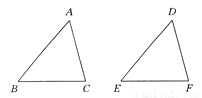
55° 50°
【解析】试题分析：在△ABC中，∠A＝180°－∠B－∠C＝55°，
由平移的性质可知：∠D＝∠A＝55°，∠E＝∠B＝50°，
故答案为：55°，50°． 三角形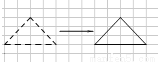
右边的是由左边的怎样平移得到的？
向右平移7个单位.
【解析】试题分析:观察图形中对应点的变化，即可得出图形的变化规律.
试题解析：
找出对应点来后会发现右边的图形是由左边的向右平移7个单位长度得到的.