题目内容
9.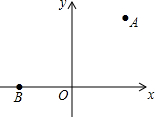 如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).
如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).(1)只用直尺(没有刻度)和圆规按下列要求作图.
(要求:保留作图痕迹,不必写出作法)
Ⅰ)AC⊥y轴,垂足为C;
Ⅱ)连结AO,AB,设边AB,CO交点E.
(2)在(1)作出图形后,直接判断△AOE与△BOE的面积大小关系.
分析 (1)过点A作AC⊥y轴于C,连接AB交y轴于E,如图,
(2)证明△ACE≌△BOE,则AE=BE,于是根据三角形面积公式可判断△AOE的面积与△BOE的面积相等.
解答 解:(1)如图,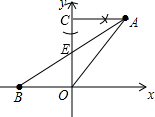
(2)∵A(3,4),B(-3,0),
∴AC=OB=3,
在△ACE和△BOE中,
$\left\{\begin{array}{l}{∠AEC=∠BEO}\\{∠ACE=∠BOE}\\{AC=BO}\end{array}\right.$,
∴△ACE≌△BOE,
∴AE=BE,
∴△AOE的面积与△BOE的面积相等.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
14.下列计算错误的有( )
①(2x+y)2=4x2+y2
②(-3b-a)(a-3b)=a2-9b2
③2×2-2=$\frac{1}{2}$
④(-1)0=-1
⑤(x-$\frac{1}{2}$)2=x2-2x+$\frac{1}{4}$
⑥(-a2)m=(-am)2.
①(2x+y)2=4x2+y2
②(-3b-a)(a-3b)=a2-9b2
③2×2-2=$\frac{1}{2}$
④(-1)0=-1
⑤(x-$\frac{1}{2}$)2=x2-2x+$\frac{1}{4}$
⑥(-a2)m=(-am)2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18. 实数a,b在数轴上的对应点的位置如图所示,化简|a-b|的结果是( )
实数a,b在数轴上的对应点的位置如图所示,化简|a-b|的结果是( )
 实数a,b在数轴上的对应点的位置如图所示,化简|a-b|的结果是( )
实数a,b在数轴上的对应点的位置如图所示,化简|a-b|的结果是( )| A. | 0 | B. | a+b | C. | a-b | D. | b-a |
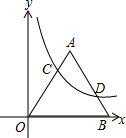 在平面直角坐标系中,等边三角形OAB中OB在x轴上,点A在第一象限,双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C,交AB于点D,若OC:BD=2:1,则OB=5.
在平面直角坐标系中,等边三角形OAB中OB在x轴上,点A在第一象限,双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C,交AB于点D,若OC:BD=2:1,则OB=5. 如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则:
如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则: 如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( )
如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( ) 已知Rt△ABC中,∠BAC=90°,M为AC的中点,N为BM中点,AN延长线交BC于P,过P作PQ∥AB交BM于Q.求证:
已知Rt△ABC中,∠BAC=90°,M为AC的中点,N为BM中点,AN延长线交BC于P,过P作PQ∥AB交BM于Q.求证: 如图,矩形OMPN的顶点O在原点,M、N分别在x轴和y轴的正半轴上,OM=6,ON=3,反比例函数y=$\frac{6}{x}$的图象与PN交于C,与PM交于D,过点C作CA⊥x轴于点A,过点D作DB⊥y轴于点B,AC与BD交于点G.
如图,矩形OMPN的顶点O在原点,M、N分别在x轴和y轴的正半轴上,OM=6,ON=3,反比例函数y=$\frac{6}{x}$的图象与PN交于C,与PM交于D,过点C作CA⊥x轴于点A,过点D作DB⊥y轴于点B,AC与BD交于点G.