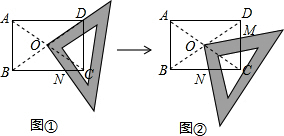
��Ŀ����
19�� ��ͼ������OMPN�Ķ���O��ԭ�㣬M��N�ֱ���x���y����������ϣ�OM=6��ON=3������������y=$\frac{6}{x}$��ͼ����PN����C����PM����D������C��CA��x���ڵ�A������D��DB��y���ڵ�B��AC��BD���ڵ�G��
��ͼ������OMPN�Ķ���O��ԭ�㣬M��N�ֱ���x���y����������ϣ�OM=6��ON=3������������y=$\frac{6}{x}$��ͼ����PN����C����PM����D������C��CA��x���ڵ�A������D��DB��y���ڵ�B��AC��BD���ڵ�G����1����֤��AB��CD��
��2����ֱ������ƽ�����Ƿ������ڵ�E��ʹ��B��C��D��EΪ���㣬BCΪ���������ǵ������Σ������ڣ����E�����ꣻ����������˵�����ɣ�
���� ��1���������C��D�����֤꣬��$\frac{AG}{GC}$=$\frac{BG}{GD}$����֤�ã�
��2���ֳ�PN��DB��CD��AB��������������ۣ�������⣮
��� ��1��֤�������ı���OMPN�Ǿ��Σ�OM=6��ON=3��
��P�������ǣ�6��3����
�ߵ�C��D���ڷ���������y=$\frac{6}{x}$��ͼ���ϣ��ҵ�C��PN�ϣ���D��PM�ϣ�
���C��2��3������D��6��1����
�֡�DB��y�ᣬCA��x�ᣬ
��A�������ǣ�2��0����B�������ǣ�0��1����
��BG=2��GD=4��CG=2��AG=1��
��$\frac{AG}{GC}$=$\frac{1}{2}$��$\frac{BG}{GD}$=$\frac{2}{4}$=$\frac{1}{2}$��
��$\frac{AG}{GC}$=$\frac{BG}{GD}$��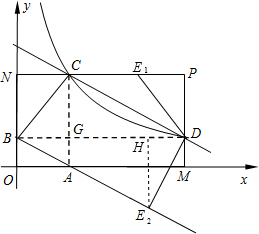
��AB��CD��
��2���⣺�١�PN��DB��
�൱DE1=BCʱ���ı���BCE1D�ǵ������Σ���ʱֱ�ǡ�CNB��ֱ�ǡ�E1PD��
��PE1=CN=2��
���E1�������ǣ�4��3����
�ڡ�CD��AB����E2��ֱ��AB�ϣ�DE2=BC=2$\sqrt{2}$���ı���BCDE2Ϊ�������Σ�
ֱ��AB�Ľ���ʽ��y=-$\frac{1}{2}$x+1��
�����E2��x��-$\frac{1}{2}$x+1����DE2=BC=2$\sqrt{2}$��
�ࣨx-6��2+��$\frac{1}{2}$x��2=8��
��ã�x1=$\frac{28}{5}$��x2=4����ȥ����
��E2�������ǣ�$\frac{28}{5}$��-$\frac{9}{5}$����
���� ���⿼����ƽ���ߵ��ж������������ε��ж������ʣ���ȷ�����ν��������ǹؼ���

| A�� | 34.383��1011 | B�� | 3.4383��1012 | C�� | 3.4383��1013 | D�� | 3.4383��1011 |
| A�� | $\sqrt{2a}$ | B�� | $\sqrt{3{a}^{2}}$ | C�� | 2$\sqrt{a}$ | D�� | $\sqrt{{a}^{4}}$ |
| A�� | $\frac{1}{2}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{2}{5}$ |
 ��ͼ��ʾ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�ԲO1��O2��O3�������һ��ƽ�������ߣ���P��ԭ��O���������������������˶����ٶ�Ϊÿ��$\frac{��}{2}$����λ���ȣ����15��ʱ����P�������ǣ�������
��ͼ��ʾ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�ԲO1��O2��O3�������һ��ƽ�������ߣ���P��ԭ��O���������������������˶����ٶ�Ϊÿ��$\frac{��}{2}$����λ���ȣ����15��ʱ����P�������ǣ�������| A�� | ��15��1�� | B�� | ��15��-1�� | C�� | ��30��1�� | D�� | ��30��-1�� |
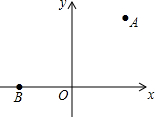 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��3��4����B��-3��0����
��ͼ����ƽ��ֱ������ϵ�У���֪��A��3��4����B��-3��0����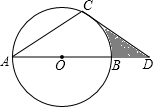 ��ͼ����D�ڡ�O��ֱ��AB���ӳ����ϣ���C�ڡ�O�ϣ�AC=CD����D=30�㣮
��ͼ����D�ڡ�O��ֱ��AB���ӳ����ϣ���C�ڡ�O�ϣ�AC=CD����D=30�㣮