题目内容
14.C是长为10cm的线段AB的黄金分割点(AC>BC),则AC=(5$\sqrt{5}$-5)cm.分析 由于点C是线段AB的黄金分割点(AC>BC),根据黄金分割的定义得到AC=$\frac{\sqrt{5}-1}{2}$AB,然后把AB=10cm代入计算即可.
解答 解:∵点C是线段AB的黄金分割点(AC>BC),
∴AC=$\frac{\sqrt{5}-1}{2}$AB,
∵AB=10cm,
∴AC=(5$\sqrt{5}$-5)cm.
故答案为:(5$\sqrt{5}$-5)cm.
点评 本题主要考查了黄金分割的定义:线段上一点把线段分成两段,其中较长线段是较短线段和整个线段的比例中项,即较长线段是整个线段的$\frac{\sqrt{5}-1}{2}$倍,那么这个点就是这条线段的黄金分割点,难度适中.

练习册系列答案
相关题目
2.借用一副三角尺,你能画出下列哪个度数的角( )
| A. | 85° | B. | 95° | C. | 105° | D. | 115° |
3.已知△ABC与△DEF相似,且对应边的比为$\sqrt{2}$:1,则△ABC与△DEF的面积比为( )
| A. | 2:1 | B. | 1:2 | C. | $\sqrt{2}$:1 | D. | 1:$\sqrt{2}$ |
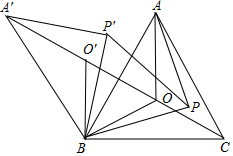 如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论:
如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论: