题目内容
19.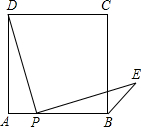 点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于45度.
点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于45度.
分析 在AD上取一点F,使DF=BP,连接PF,由正方形的性质就可以得出△DFP≌△PBE,就可以得出∠DFP=∠PBE,根据AP=AF就可以得出∠DFP的值,就可以求出∠CBE的值.
解答 解:在AD上取一点F,使DF=BP,连接PF,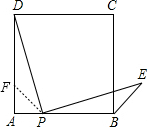
∵四边形ABCD是正方形,
∴AD=AB,∠A=∠ABC=90°.
∴AD-DF=AB-BP,∠ADP+∠APD=90°,
∴AF=AP.
∴∠AFP=∠APF=45°,
∴∠DFP=135°.
∵∠DPE=90°
∴∠APD+∠BPE=90°.
∴∠ADP=∠BPE.
在△DFP和△PBE中,
∵$\left\{\begin{array}{l}{DF=BP}\\{∠ADP=∠BPE}\\{DP=PE}\end{array}\right.$,
∴△DFP≌△PBE(SAS),
∴∠DFP=∠PBE,
∴∠PBE=135°,
∴∠EBC=135°-90°=45°.
故答案为:45.
点评 本题考查了正方形的性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
8.下列各式成立的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | ||
| C. | -x2+4xy-4xy2=-(x-2y)2 | D. | a2+ab+b2=(a+b)2 |
 如图,已知一次函数y=kx+b,则当x<2.5时,kx+b<0.
如图,已知一次函数y=kx+b,则当x<2.5时,kx+b<0.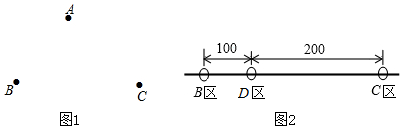
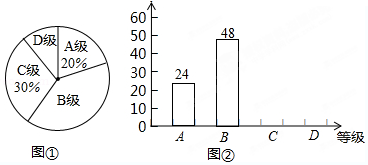
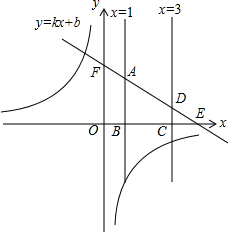 已知反比例函数y=$\frac{k}{x}$的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F
已知反比例函数y=$\frac{k}{x}$的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F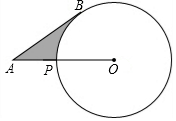 如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2
如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2 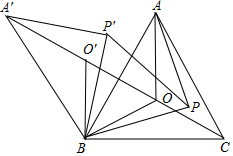 如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论:
如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论: