题目内容
19.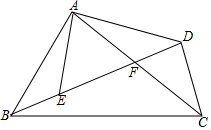 如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.
如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由.
分析 (1)先根据题意得出△ABC∽△AED,由相似三角形的性质即可得出结论;
(2)先根据题意得出$\frac{AB}{AC}$=$\frac{AE}{AD}$,再由∠BAE=∠CAD即可得出结论.
解答 解:(1)∠BAE与∠CAD相等.
理由:∵$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
(2)△ABE与△ACD相似.
∵$\frac{AB}{AE}$=$\frac{AC}{AD}$,
∴$\frac{AB}{AC}$=$\frac{AE}{AD}$.
在△ABE与△ACD中,
∵$\frac{AB}{AC}$=$\frac{AE}{AD}$,∠BAE=∠CAD,
∴△ABE∽△ACD.
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.

练习册系列答案
相关题目
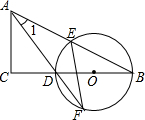 如图,△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O交AB于E,交AD的延长线于F,连结EF,∠1=∠F.
如图,△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O交AB于E,交AD的延长线于F,连结EF,∠1=∠F. 分别画出满足下列条件的点:(尺规作图,请保留组图痕迹,不写作法).
分别画出满足下列条件的点:(尺规作图,请保留组图痕迹,不写作法).