题目内容
8.解不等式组:$\left\{\begin{array}{l}{x-2>0}\\{\frac{x-3}{2}≤x+1}\end{array}\right.$.分析 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:$\left\{\begin{array}{l}{x-2>0①}\\{\frac{x-3}{2}≤x+1②}\end{array}\right.$,
由①得:x>2,
由②得:x-3≤2(x+1),
x-3≤2x+2,
x-2x≤2+3,
-x≤5,
x≥-5,
所以原不等式组的解集为:x>2.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 如图,C,D是线段AB上两点,D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长等于多少?
如图,C,D是线段AB上两点,D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长等于多少?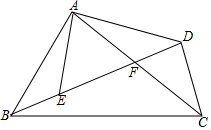 如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.
如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$. 已知:如图,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连结BC′,求BC′的长.
已知:如图,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连结BC′,求BC′的长. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 如图,某大学计划在一块长80m,宽60m的长方形场地中央建一个长方形网球场,四周留出宽度相等的人行走道(阴影部分).设人行走道的宽为x(m),求网球场的面积.
如图,某大学计划在一块长80m,宽60m的长方形场地中央建一个长方形网球场,四周留出宽度相等的人行走道(阴影部分).设人行走道的宽为x(m),求网球场的面积.